10-01-14

12:37
[FONT=Times New Roman, serif]Αγαπητοί συνομιλητές, γειά σας.[/FONT]
[FONT=Times New Roman, serif]Ονομάζομαι Αλεξίνοος.[/FONT]
[FONT=Times New Roman, serif]Δημοσιεύω αυτό το θέμα διότι χρειάζομαι την βοήθειά σας. – Κυριολεκτώ:[/FONT]
[FONT=Times New Roman, serif]Έχω ενώπιόν μου ένα ερώτημα και κάποιες απαντήσεις του.[/FONT]
[FONT=Times New Roman, serif]Οι απαντήσεις αυτές είναι μονομερείς και ελλιπείς.[/FONT]
[FONT=Times New Roman, serif]Θέλω να τις καταστήσω πολυμερείς (πολυμερέστερες) και πλήρεις (πληρέστερες).[/FONT]
[FONT=Times New Roman, serif]Ας αρχίσω:[/FONT]
[FONT=Times New Roman, serif]Υπάρχει ένα γεωμετρικό πρόβλημα το οποίο θα αναφέρω κατόπιν.[/FONT]
[FONT=Times New Roman, serif]Υπάρχει και η, από αιώνων, διαδεδομένη πεποίθηση ότι, αυτό το πρόβλημα ...δεν έχει λύση. Αυτή η πεποίθηση δεν έχει, μέχρι τούδε, αμφισβητηθεί, εκπεφρασμένα, από κανένα.[/FONT]
[FONT=Times New Roman, serif]Το ερώτημά μου:[/FONT]
[FONT=Times New Roman, serif]Εάν το πρόβλημα αυτό έχει πολλές λύσεις, πώς έχει επικρατήσει η εν λόγω πεποίθηση;[/FONT]
[FONT=Times New Roman, serif]Σημειωτέον ότι δεν πρόκειται για κάτι το δύσκολο (όπως, π.χ., ο τετραγωνισμός του κύκλου) και ότι διά την εύρεση των λύσεών του (ή, έστω μερικών), δεν απαιτούνται ούτε ιδιαίτερες γνώσεις γεωμετρίας ούτε ιδιαίτερη ευφυία. Χρειάζεται, μόνον, η διάθεση κάποιου, να ασχοληθεί και το θάρρος του διά να μην επηρεαστεί από τις διαδόσεις. Δηλαδή, να μη φοβηθεί... Χμμμ...: Αυτό όμως, δεν είναι κι΄ εύκολο...: Π.χ., πώς να αντιδράσει σωστά, όταν ακούσει (και πιστέψει):[/FONT]
[FONT=Times New Roman, serif]«Βρε, εδώ δεν μπορούσε να το λύσει ο Θαλής... Και θα μπορέσεις, εσύ;»[/FONT]
[FONT=Times New Roman, serif]Η σωστή αντίδραση είναι να πει:[/FONT]
[FONT=Times New Roman, serif]«Εάν όμως, εγώ, μπορέσω, να το λύσω, τότε, εσύ, που λες πως δεν μπορούσε ο Θαλής, ψεύδεσαι.»[/FONT]
[FONT=Times New Roman, serif]Και ίσως να προσθέσει:[/FONT]
[FONT=Times New Roman, serif]«Και διά του ψεύδους σου, με φοβίζεις και με αποτρέπεις από του να ασχοληθώ...»[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Δεν αποδίδω προθέσεις. Περιγράφω αποτελέσματα... Πάντως, η έκφραση «τα έχει πάρει από φόβο», όταν λέγεται διά τα μαθηματικά, είναι τόσο αφύσικη ώστε δεν μπορεί να έχει προκύψει χωρίς κάποια επέμβαση που την έχει προκαλέσει.[/FONT]
[FONT=Times New Roman, serif]Παρατήρηση:[/FONT]
[FONT=Times New Roman, serif]Αυτή είναι, ήδη, μία απάντηση: Ελλιπής, μονομερής και, ίσως, υπαγορευμένη από μία δική μου προκατάληψη. Εξ ου και η ανάγκη μίας ευρύτερης συζήτησης.[/FONT]
[FONT=Times New Roman, serif]Το πρόβλημα:[/FONT]
[FONT=Times New Roman, serif]Πολλοί έχουν ακούσει ότι, ο Θαλής, μέτρησε το ύψος της Πυραμίδος του Χέοπος, χρησιμοποιώντας την σκιά της. Λέγεται όμως ότι, αυτό, δεν μπορούσε να το πραγματοποιήσει οποιαδήποτε στιγμή: Έπρεπε πρώτα να επιλύσει ένα γεωμετρικό πρόβλημα. Ας δούμε, ποίο ήταν το πρόβλημα αυτό και, κατόπιν, θα πούμε διά τι του ήταν απαραίτητη, η λύση του, προκειμένου να προχωρήσει.[/FONT]
[FONT=Times New Roman, serif]Η “διάδοση” λέγει:[/FONT]
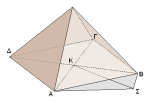
[FONT=Times New Roman, serif]Την βλέπετε αυτή την πυραμίδα (στο σχήμα που θα ακολουθήσει), την βάση της, την ΑΒΓΔ, την σκιά της, την ΑΣΒ και την κορυφή της σκιάς, την Σ;[/FONT]
[FONT=Times New Roman, serif]Ε, ο Θαλής δεν μπορούσε να βρει την απόσταση του Σ από το κέντρο Κ, του τετραγώνου ΑΒΓΔ, διότι, ένα τμήμα της ήταν πλακωμένο από την πυραμίδα.[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Εις το σημείο αυτό, ένας αναγνώστης, μπορεί να πει κάποια λόγια σαν κι΄ αυτά:[/FONT]
[FONT=Times New Roman, serif]«Και, γιατί – παρακαλώ – δεν μπορούσε, ο Θαλής, να βρει την ΣΚ; –Βρε, για ό,τι και να την ήθελε... “δεν σηκώνει” να μου λες τέτοια πράγματα...»[/FONT]
[FONT=Times New Roman, serif]Αυτός, λοιπόν, μπορεί, να δοκιμάζει ο ίδιος να την βρει, και, μάλιστα, χωρίς κάποιο “ισχυρό κίνητρο” – έτσι, “για πλάκα”. Εάν επιτύχει, θα έχουμε μία ισχυρή ένδειξη πως το «άλυτο πρόβλημα», στην πραγματικότητα, ήταν “της πλάκας”.[/FONT]
[FONT=Times New Roman, serif]Έ, ας διακόψουμε, ώστε να του δώσουμε τον χρόνο να το πράξει... Και, έπειτα, ας μας πει εάν έχει δίκιο ο Θαλής όταν λέγει:[/FONT]
[FONT=Times New Roman, serif]«Τί ήδιστον; Το επιτυγχάνειν.»[/FONT]
[FONT=Times New Roman, serif]Υ.Γ.:[/FONT]
[FONT=Times New Roman, serif]Εάν, ώσπου να παρουσιάσω τις λύσεις, κάποιοι αναγνώστες προτείνουν άλλες λύσεις (ή, και τις ίδιες), τότε το τεθέν ερώτημα θα γίνει εντονότερο.[/FONT]
[FONT=Times New Roman, serif]Ονομάζομαι Αλεξίνοος.[/FONT]
[FONT=Times New Roman, serif]Δημοσιεύω αυτό το θέμα διότι χρειάζομαι την βοήθειά σας. – Κυριολεκτώ:[/FONT]
[FONT=Times New Roman, serif]Έχω ενώπιόν μου ένα ερώτημα και κάποιες απαντήσεις του.[/FONT]
[FONT=Times New Roman, serif]Οι απαντήσεις αυτές είναι μονομερείς και ελλιπείς.[/FONT]
[FONT=Times New Roman, serif]Θέλω να τις καταστήσω πολυμερείς (πολυμερέστερες) και πλήρεις (πληρέστερες).[/FONT]
[FONT=Times New Roman, serif]Ας αρχίσω:[/FONT]
[FONT=Times New Roman, serif]Υπάρχει ένα γεωμετρικό πρόβλημα το οποίο θα αναφέρω κατόπιν.[/FONT]
[FONT=Times New Roman, serif]Υπάρχει και η, από αιώνων, διαδεδομένη πεποίθηση ότι, αυτό το πρόβλημα ...δεν έχει λύση. Αυτή η πεποίθηση δεν έχει, μέχρι τούδε, αμφισβητηθεί, εκπεφρασμένα, από κανένα.[/FONT]
[FONT=Times New Roman, serif]Το ερώτημά μου:[/FONT]
[FONT=Times New Roman, serif]Εάν το πρόβλημα αυτό έχει πολλές λύσεις, πώς έχει επικρατήσει η εν λόγω πεποίθηση;[/FONT]
[FONT=Times New Roman, serif]Σημειωτέον ότι δεν πρόκειται για κάτι το δύσκολο (όπως, π.χ., ο τετραγωνισμός του κύκλου) και ότι διά την εύρεση των λύσεών του (ή, έστω μερικών), δεν απαιτούνται ούτε ιδιαίτερες γνώσεις γεωμετρίας ούτε ιδιαίτερη ευφυία. Χρειάζεται, μόνον, η διάθεση κάποιου, να ασχοληθεί και το θάρρος του διά να μην επηρεαστεί από τις διαδόσεις. Δηλαδή, να μη φοβηθεί... Χμμμ...: Αυτό όμως, δεν είναι κι΄ εύκολο...: Π.χ., πώς να αντιδράσει σωστά, όταν ακούσει (και πιστέψει):[/FONT]
[FONT=Times New Roman, serif]«Βρε, εδώ δεν μπορούσε να το λύσει ο Θαλής... Και θα μπορέσεις, εσύ;»[/FONT]
[FONT=Times New Roman, serif]Η σωστή αντίδραση είναι να πει:[/FONT]
[FONT=Times New Roman, serif]«Εάν όμως, εγώ, μπορέσω, να το λύσω, τότε, εσύ, που λες πως δεν μπορούσε ο Θαλής, ψεύδεσαι.»[/FONT]
[FONT=Times New Roman, serif]Και ίσως να προσθέσει:[/FONT]
[FONT=Times New Roman, serif]«Και διά του ψεύδους σου, με φοβίζεις και με αποτρέπεις από του να ασχοληθώ...»[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Δεν αποδίδω προθέσεις. Περιγράφω αποτελέσματα... Πάντως, η έκφραση «τα έχει πάρει από φόβο», όταν λέγεται διά τα μαθηματικά, είναι τόσο αφύσικη ώστε δεν μπορεί να έχει προκύψει χωρίς κάποια επέμβαση που την έχει προκαλέσει.[/FONT]
[FONT=Times New Roman, serif]Παρατήρηση:[/FONT]
[FONT=Times New Roman, serif]Αυτή είναι, ήδη, μία απάντηση: Ελλιπής, μονομερής και, ίσως, υπαγορευμένη από μία δική μου προκατάληψη. Εξ ου και η ανάγκη μίας ευρύτερης συζήτησης.[/FONT]
[FONT=Times New Roman, serif]Το πρόβλημα:[/FONT]
[FONT=Times New Roman, serif]Πολλοί έχουν ακούσει ότι, ο Θαλής, μέτρησε το ύψος της Πυραμίδος του Χέοπος, χρησιμοποιώντας την σκιά της. Λέγεται όμως ότι, αυτό, δεν μπορούσε να το πραγματοποιήσει οποιαδήποτε στιγμή: Έπρεπε πρώτα να επιλύσει ένα γεωμετρικό πρόβλημα. Ας δούμε, ποίο ήταν το πρόβλημα αυτό και, κατόπιν, θα πούμε διά τι του ήταν απαραίτητη, η λύση του, προκειμένου να προχωρήσει.[/FONT]
[FONT=Times New Roman, serif]Η “διάδοση” λέγει:[/FONT]
[FONT=Times New Roman, serif]Την βλέπετε αυτή την πυραμίδα (στο σχήμα που θα ακολουθήσει), την βάση της, την ΑΒΓΔ, την σκιά της, την ΑΣΒ και την κορυφή της σκιάς, την Σ;[/FONT]
[FONT=Times New Roman, serif]Ε, ο Θαλής δεν μπορούσε να βρει την απόσταση του Σ από το κέντρο Κ, του τετραγώνου ΑΒΓΔ, διότι, ένα τμήμα της ήταν πλακωμένο από την πυραμίδα.[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Εις το σημείο αυτό, ένας αναγνώστης, μπορεί να πει κάποια λόγια σαν κι΄ αυτά:[/FONT]
[FONT=Times New Roman, serif]«Και, γιατί – παρακαλώ – δεν μπορούσε, ο Θαλής, να βρει την ΣΚ; –Βρε, για ό,τι και να την ήθελε... “δεν σηκώνει” να μου λες τέτοια πράγματα...»[/FONT]
[FONT=Times New Roman, serif]Αυτός, λοιπόν, μπορεί, να δοκιμάζει ο ίδιος να την βρει, και, μάλιστα, χωρίς κάποιο “ισχυρό κίνητρο” – έτσι, “για πλάκα”. Εάν επιτύχει, θα έχουμε μία ισχυρή ένδειξη πως το «άλυτο πρόβλημα», στην πραγματικότητα, ήταν “της πλάκας”.[/FONT]
[FONT=Times New Roman, serif]Έ, ας διακόψουμε, ώστε να του δώσουμε τον χρόνο να το πράξει... Και, έπειτα, ας μας πει εάν έχει δίκιο ο Θαλής όταν λέγει:[/FONT]
[FONT=Times New Roman, serif]«Τί ήδιστον; Το επιτυγχάνειν.»[/FONT]
[FONT=Times New Roman, serif]Υ.Γ.:[/FONT]
[FONT=Times New Roman, serif]Εάν, ώσπου να παρουσιάσω τις λύσεις, κάποιοι αναγνώστες προτείνουν άλλες λύσεις (ή, και τις ίδιες), τότε το τεθέν ερώτημα θα γίνει εντονότερο.[/FONT]
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα

13-01-14

12:23
[FONT=Times New Roman, serif]Μία απλή σκέψη:[/FONT]
[FONT=Times New Roman, serif]Συμφώνως προς ορισμένα ιστορικά στοιχεία (θα τα αναφέρω αν μου ζητηθεί), ο Θαλής, θέλοντας να υπολογίσει το ύψος της Πυραμίδος του Χέοπος, εσκέφθη κάτι απλό, κάτι, που μπορεί να το σκεφθεί ο καθείς, χωρίς να είναι και ...“Θαλής”: Αρκεί να είναι νοήμων – ας είναι, εντελώς, αγεωμέτρητος – και να έχει παρατηρήσει ότι τα διάφορα αντικείμενα, “ρίχνουν” σκιά, κατά τρόπον ανάλογον (ανά λόγον) προς το ύψος τους. Π.χ., όποιος δει ότι το ραβδί του, που έχει μήκος 1μ, όταν είναι κατακόρυφο, “ρίχνει” σκιά μήκους 1,5μ και, ταυτοχρόνως, μετρήσει το μήκος της σκιάς ενός στύλου της ΔΕΗ και το βρει 15μ, αμέσως θα συμπεράνει ότι το μήκος του στύλου είναι 10μ.[/FONT]
[FONT=Times New Roman, serif]Εάν όμως, ο στύλος ήταν στη θέση του ύψους μίας πυραμίδος, δηλαδή, εάν ήταν “κτισμένος” μέσα σε αυτήν, τότε, ο αγεωμέτρητος θα δυσκολευόταν, διότι δεν θα μπορούσε να μετρήσει το μήκος της σκιάς του που ήταν “πλακωμένο” από την πυραμίδα – έστω και αν, η πυραμίδα, ήταν κανονική, τετραγωνική.[/FONT]
[FONT=Times New Roman, serif]Εάν ο νοήμων αγεωμέτρητος πει: «εγώ, δεν μπορώ να υπολογίσω το μήκος της “πλακωμένης” σκιάς», δεν θα έπαυε να είναι νοήμων. Αλλά, θα ήταν ανόητος, εάν έλεγε: «ο Θαλής δεν μπορούσε»...[/FONT]
[FONT=Times New Roman, serif]Σημείωση – παρατήρηση:[/FONT]
[FONT=Times New Roman, serif]Πάντως, μία τέτοια δήλωση είναι απαράδεχτη για κάποιον μαθηματικό. Αυτός, δεν επιτρέπεται να πει ότι, κάτι, «δεν γίνεται», χωρίς να το αποδείξει. Και, προφανώς, δεν είναι απόδειξη η δική του αδυναμία (ή, η αμέλεια). Άρα, όταν λέγει πως «ο Θαλής δεν μπορούσε» εννοεί ότι: [FONT=Times New Roman, serif]«[/FONT][FONT=Times New Roman, serif]είτε γίνεται, είτε δεν γίνεται, ο Θαλής δεν μπορούσε[/FONT][FONT=Times New Roman, serif]». Αυτό ας μη το σχολιάσουμε...[/FONT][/FONT]
[FONT=Times New Roman, serif]Δεδομένου ότι, ο Θαλής υπελόγισε το ύψος της πυραμίδος, αυτός που αδυνατεί να σκεφθεί πώς το έπραξε, προσπαθεί να επινοήσει κάποιο “κολπάκι” το οποίο, δήθεν, θα πρέπει να έχει κάμει εκείνος, ώστε να το επιτύχει.[/FONT]
“[FONT=Times New Roman, serif]Σου λέει”, λοιπόν :[/FONT]
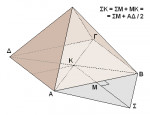
[FONT=Times New Roman, serif]«Όταν η διεύθυνση των ακτίνων του ήλιου σχηματίζει μία τυχαία γωνία με μία πλευρά ΑΒ της βάσης ΑΒΓΔ της πυραμίδας (σχήμα προηγουμένου μηνύματος), η σκιά της σχηματίζει ένα τυχαίο τρίγωνο το ΑΣΒ και... ο Θαλής, δεν μπορεί να κάνει τίποτα, γιατί η ΣΚ (όπου Κ το κέντρο του ΑΒΓΔ) είναι “λοξή”. Εάν η ΣΚ ήταν κάθετη προς την ΑΒ (σχήμα που ακολουθεί), τότε, το κρυμμένο μέρος της, θα ήταν ίσο με την μισή πλευρά της βάσης...».[/FONT]
[FONT=Times New Roman, serif]Αυτό είναι το διαδεδομένο “σενάριο”, το οποίο δεν έχει αμφισβητηθεί (δεδηλωμένα), μέχρι τούδε.[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Προτού να συνεχίσω (στο επόμενο μήνυμα) θα υπενθυμίσω κάτι που έχει πει ο Επίχαρμος:[/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]«[/FONT][FONT=Times New Roman, serif]Νήφε και μέμνησο απιστείν[/FONT][FONT=Times New Roman, serif]», δηλαδή να είσαι νηφάλιος και να θυμάσαι να δυσπιστείς. Το θέμα δεν είναι αν πρέπει να είμαστε “δύσπιστοι” ή, “εύπιστοι” αλλά, να ενεργούμε με νηφαλιότητα.[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]...[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Ας εξετάσουμε, λοιπόν, με νηφαλιότητα το κατά πόσον ευσταθεί το εν λόγω σενάριο...:[/FONT][/FONT]
[FONT=Times New Roman, serif]Συμφώνως προς ορισμένα ιστορικά στοιχεία (θα τα αναφέρω αν μου ζητηθεί), ο Θαλής, θέλοντας να υπολογίσει το ύψος της Πυραμίδος του Χέοπος, εσκέφθη κάτι απλό, κάτι, που μπορεί να το σκεφθεί ο καθείς, χωρίς να είναι και ...“Θαλής”: Αρκεί να είναι νοήμων – ας είναι, εντελώς, αγεωμέτρητος – και να έχει παρατηρήσει ότι τα διάφορα αντικείμενα, “ρίχνουν” σκιά, κατά τρόπον ανάλογον (ανά λόγον) προς το ύψος τους. Π.χ., όποιος δει ότι το ραβδί του, που έχει μήκος 1μ, όταν είναι κατακόρυφο, “ρίχνει” σκιά μήκους 1,5μ και, ταυτοχρόνως, μετρήσει το μήκος της σκιάς ενός στύλου της ΔΕΗ και το βρει 15μ, αμέσως θα συμπεράνει ότι το μήκος του στύλου είναι 10μ.[/FONT]
[FONT=Times New Roman, serif]Εάν όμως, ο στύλος ήταν στη θέση του ύψους μίας πυραμίδος, δηλαδή, εάν ήταν “κτισμένος” μέσα σε αυτήν, τότε, ο αγεωμέτρητος θα δυσκολευόταν, διότι δεν θα μπορούσε να μετρήσει το μήκος της σκιάς του που ήταν “πλακωμένο” από την πυραμίδα – έστω και αν, η πυραμίδα, ήταν κανονική, τετραγωνική.[/FONT]
[FONT=Times New Roman, serif]Εάν ο νοήμων αγεωμέτρητος πει: «εγώ, δεν μπορώ να υπολογίσω το μήκος της “πλακωμένης” σκιάς», δεν θα έπαυε να είναι νοήμων. Αλλά, θα ήταν ανόητος, εάν έλεγε: «ο Θαλής δεν μπορούσε»...[/FONT]
[FONT=Times New Roman, serif]Σημείωση – παρατήρηση:[/FONT]
[FONT=Times New Roman, serif]Πάντως, μία τέτοια δήλωση είναι απαράδεχτη για κάποιον μαθηματικό. Αυτός, δεν επιτρέπεται να πει ότι, κάτι, «δεν γίνεται», χωρίς να το αποδείξει. Και, προφανώς, δεν είναι απόδειξη η δική του αδυναμία (ή, η αμέλεια). Άρα, όταν λέγει πως «ο Θαλής δεν μπορούσε» εννοεί ότι: [FONT=Times New Roman, serif]«[/FONT][FONT=Times New Roman, serif]είτε γίνεται, είτε δεν γίνεται, ο Θαλής δεν μπορούσε[/FONT][FONT=Times New Roman, serif]». Αυτό ας μη το σχολιάσουμε...[/FONT][/FONT]
[FONT=Times New Roman, serif]Δεδομένου ότι, ο Θαλής υπελόγισε το ύψος της πυραμίδος, αυτός που αδυνατεί να σκεφθεί πώς το έπραξε, προσπαθεί να επινοήσει κάποιο “κολπάκι” το οποίο, δήθεν, θα πρέπει να έχει κάμει εκείνος, ώστε να το επιτύχει.[/FONT]
“[FONT=Times New Roman, serif]Σου λέει”, λοιπόν :[/FONT]
[FONT=Times New Roman, serif]«Όταν η διεύθυνση των ακτίνων του ήλιου σχηματίζει μία τυχαία γωνία με μία πλευρά ΑΒ της βάσης ΑΒΓΔ της πυραμίδας (σχήμα προηγουμένου μηνύματος), η σκιά της σχηματίζει ένα τυχαίο τρίγωνο το ΑΣΒ και... ο Θαλής, δεν μπορεί να κάνει τίποτα, γιατί η ΣΚ (όπου Κ το κέντρο του ΑΒΓΔ) είναι “λοξή”. Εάν η ΣΚ ήταν κάθετη προς την ΑΒ (σχήμα που ακολουθεί), τότε, το κρυμμένο μέρος της, θα ήταν ίσο με την μισή πλευρά της βάσης...».[/FONT]
[FONT=Times New Roman, serif]Αυτό είναι το διαδεδομένο “σενάριο”, το οποίο δεν έχει αμφισβητηθεί (δεδηλωμένα), μέχρι τούδε.[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Προτού να συνεχίσω (στο επόμενο μήνυμα) θα υπενθυμίσω κάτι που έχει πει ο Επίχαρμος:[/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]«[/FONT][FONT=Times New Roman, serif]Νήφε και μέμνησο απιστείν[/FONT][FONT=Times New Roman, serif]», δηλαδή να είσαι νηφάλιος και να θυμάσαι να δυσπιστείς. Το θέμα δεν είναι αν πρέπει να είμαστε “δύσπιστοι” ή, “εύπιστοι” αλλά, να ενεργούμε με νηφαλιότητα.[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]...[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Ας εξετάσουμε, λοιπόν, με νηφαλιότητα το κατά πόσον ευσταθεί το εν λόγω σενάριο...:[/FONT][/FONT]
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
Dimitris_SM
Εκκολαπτόμενο μέλος
Ο Dimitris_SM αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 30 ετών. Έχει γράψει 225 μηνύματα.

13-01-14

20:42
χ=5
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

16-01-14

14:28
[FONT=Times New Roman, serif]Οι τέσσαρες προϋποθέσεις του “σεναρίου” (Α μέρος):[/FONT]
[FONT=Times New Roman, serif]Το σενάριο που αναφέρεται εις το #2 τελεί υπό τέσσαρες προϋποθέσεις [FONT=Times New Roman, serif]τις οποίες είμαστε υποχρεωμένοι να αναφέρουμε, επειδή, άνευ αυτών, ο Θαλής δεν θα μπορούσε να είχε υπολογίσει το ύψος της με τόση μεγάλη ακρίβεια (σχεδόν 99%).[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Οι εν λόγω προϋποθέσεις, όπως θα δούμε είναι ...ανέφικτες (εκτός της 1ης που είναι ...μισοεφικτή). Αυτό σημαίνει ότι, ο Θαλής, προκειμένου να “μαθηματικοποιήσει” το πρόβλημα ώστε να το επιλύσει, είτε τις υποκατέστησε με άλλες ή, ακολούθησε άλλη μέθοδο.[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Θα περιγράψουμε τις προϋποθέσεις αυτές, θα εξηγήσουμε το ανέφικτο και, κατόπιν, ...θα τις δεχθούμε. Αυτό θα γίνει διότι, διά της εν λόγω παραδοχής, αποκτούμε ένα ενδιαφέρον πεδίο γεωμετρικής/νοητικής (εξ)άσκησης.[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Άλλωστε, το θέμα αυτής της δημοσίευσης δεν είναι το αν ορθώς πιστεύεται ότι ο Θαλής εφήρμοσε την μέθοδο της σκιάς αλλά, το εξής:[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Υποτιθεμένου ότι εφήρμοσε, την μέθοδο αυτήν, πως πιστεύεται ότι δεν μπορούσε να υπολογίσει την [/FONT][FONT=Times New Roman, serif]ΣΚ[/FONT][FONT=Times New Roman, serif] που αναφέρεται εις το [/FONT][FONT=Times New Roman, serif]#1[/FONT][FONT=Times New Roman, serif].[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]1η προϋπόθεση:[/FONT][/FONT]
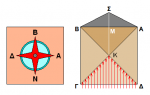
[FONT=Times New Roman, serif]Διά να είναι η σκιά του ύψους της Πυραμίδος του Χέοπος κάθετη προς μία πλευρά της βάσεώς της ΑΒΓΔ, έστω της ΑΒ, θα πρέπει, προφανώς οι ηλιακές ακτίνες να είναι κάθετες επί την πλευρά αυτήν.[/FONT]
[FONT=Times New Roman, serif]Δοθέντος ότι η πυραμίδα είναι κτισμένη κατά τρόπον ώστε δύο πλευρές της βάσεώς της, έστω οι ΒΓ και ΔΑ, να έχουν κατεύθυνση Βορρά-Νότου, το προηγούμενο, συμβαίνει κατά την μεσημβρίαν, όταν ο Ήλιος μεσουρανεί, δηλαδή, όταν ευρίσκεται εντός του επιπέδου του μεσημβρινού που διέρχεται από την Γκίζα, όπου είναι και η πυραμίς (βλέπε σχήμα).[/FONT]
[FONT=Times New Roman, serif]Αλλά, όταν ο Ήλιος μεσουρανεί, η πυραμίς ενδέχεται να ...μη “ρίχνει” ορατή σκιά, δηλαδή, σκιά εκτός της βάσεως ΑΒΓΔ.[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Εδώ, ας διακόψουμε ώστε να δοθεί η ευκαιρία σε όσους θέλουν να εξετάσουν την τελευταία φράση:[/FONT]
[FONT=Times New Roman, serif]Πότε, δηλαδή, συμβαίνει, η πυραμίς, να ρίχνει σκιά και πότε όχι.[/FONT]
[FONT=Times New Roman, serif]Το σενάριο που αναφέρεται εις το #2 τελεί υπό τέσσαρες προϋποθέσεις [FONT=Times New Roman, serif]τις οποίες είμαστε υποχρεωμένοι να αναφέρουμε, επειδή, άνευ αυτών, ο Θαλής δεν θα μπορούσε να είχε υπολογίσει το ύψος της με τόση μεγάλη ακρίβεια (σχεδόν 99%).[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Οι εν λόγω προϋποθέσεις, όπως θα δούμε είναι ...ανέφικτες (εκτός της 1ης που είναι ...μισοεφικτή). Αυτό σημαίνει ότι, ο Θαλής, προκειμένου να “μαθηματικοποιήσει” το πρόβλημα ώστε να το επιλύσει, είτε τις υποκατέστησε με άλλες ή, ακολούθησε άλλη μέθοδο.[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Θα περιγράψουμε τις προϋποθέσεις αυτές, θα εξηγήσουμε το ανέφικτο και, κατόπιν, ...θα τις δεχθούμε. Αυτό θα γίνει διότι, διά της εν λόγω παραδοχής, αποκτούμε ένα ενδιαφέρον πεδίο γεωμετρικής/νοητικής (εξ)άσκησης.[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Άλλωστε, το θέμα αυτής της δημοσίευσης δεν είναι το αν ορθώς πιστεύεται ότι ο Θαλής εφήρμοσε την μέθοδο της σκιάς αλλά, το εξής:[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Υποτιθεμένου ότι εφήρμοσε, την μέθοδο αυτήν, πως πιστεύεται ότι δεν μπορούσε να υπολογίσει την [/FONT][FONT=Times New Roman, serif]ΣΚ[/FONT][FONT=Times New Roman, serif] που αναφέρεται εις το [/FONT][FONT=Times New Roman, serif]#1[/FONT][FONT=Times New Roman, serif].[/FONT][/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]1η προϋπόθεση:[/FONT][/FONT]
[FONT=Times New Roman, serif]Διά να είναι η σκιά του ύψους της Πυραμίδος του Χέοπος κάθετη προς μία πλευρά της βάσεώς της ΑΒΓΔ, έστω της ΑΒ, θα πρέπει, προφανώς οι ηλιακές ακτίνες να είναι κάθετες επί την πλευρά αυτήν.[/FONT]
[FONT=Times New Roman, serif]Δοθέντος ότι η πυραμίδα είναι κτισμένη κατά τρόπον ώστε δύο πλευρές της βάσεώς της, έστω οι ΒΓ και ΔΑ, να έχουν κατεύθυνση Βορρά-Νότου, το προηγούμενο, συμβαίνει κατά την μεσημβρίαν, όταν ο Ήλιος μεσουρανεί, δηλαδή, όταν ευρίσκεται εντός του επιπέδου του μεσημβρινού που διέρχεται από την Γκίζα, όπου είναι και η πυραμίς (βλέπε σχήμα).[/FONT]
[FONT=Times New Roman, serif]Αλλά, όταν ο Ήλιος μεσουρανεί, η πυραμίς ενδέχεται να ...μη “ρίχνει” ορατή σκιά, δηλαδή, σκιά εκτός της βάσεως ΑΒΓΔ.[/FONT]
[FONT=Times New Roman, serif]...[/FONT]
[FONT=Times New Roman, serif]Εδώ, ας διακόψουμε ώστε να δοθεί η ευκαιρία σε όσους θέλουν να εξετάσουν την τελευταία φράση:[/FONT]
[FONT=Times New Roman, serif]Πότε, δηλαδή, συμβαίνει, η πυραμίς, να ρίχνει σκιά και πότε όχι.[/FONT]
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα

17-01-14

18:11
[FONT=Times New Roman, serif]Οι τέσσαρες προϋποθέσεις του “σεναρίου” (Β μέρος):[/FONT]
[FONT=Times New Roman, serif]Εν όσω κάποιοι αναγνώστες μπορεί να εξετάζουν το θέμα που ετέθη εις το τέλος του προηγουμένου μηνύματος, ήτοι, το [FONT=Times New Roman, serif]«π[/FONT]ότε συμβαίνει, η πυραμίς, να “ρίχνει” σκιά και πότε, όχι[FONT=Times New Roman, serif]»[/FONT], ας διατυπώσουμε τις υπόλοιπες τρεις προϋποθέσεις. Αυτές, θέτουν εν αμφιβόλω την όλη πεποίθηση ότι, ο Θαλής, χρησιμοποίησε την μέθοδο της σκιάς. Εν τούτοις, θα τις δεχθούμε διά τους λόγους που εξηγήσαμε, ήδη (εις το εν λόγω μήνυμα). Εκείνο που θα απορρίψουμε είναι το “σενάριο” ότι χρησιμοποίησε την σκιά του ύψους όταν, αυτή, ήταν κάθετη προς μία πλευρά της βάσεως της πυραμίδος. Θα αποδείξουμε ότι, κάτι τέτοιο, είναι [FONT=Times New Roman, serif]αντιφατικό ή/και παράλογο. Αυτό θα γίνει αφού έχουμε εξετάσει ικανοποιητικώς την, εν λόγω, κάθετη [/FONT]“ρίψη” της σκιάς[FONT=Times New Roman, serif] ([/FONT]εις το επόμενο μήνυμα[FONT=Times New Roman, serif])[/FONT].[/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Ας συνεχίσουμε:[/FONT][/FONT]
[FONT=Times New Roman, serif]2α προϋπόθεση:[/FONT]
[FONT=Times New Roman, serif]Το φαινόμενο της περιθλάσεως του φωτός ...δεν συμβαίνει.[/FONT]
–[FONT=Times New Roman, serif]Ως προς το αν συμβαίνει αυτό, αρκεί μία απλή παρατήρηση: Εάν δούμε την σκιά που “ρίχνει” (π.χ.) ένας στύλος της ΔΕΗ, θα παρατηρήσουμε ότι καθώς αυτή απομακρύνεται από την βάση του στύλου, γίνεται όλο και πιο ασαφής, πιο “θαμπή”. Η δε σκιά της κορυφής του, δεν έχει κάποιο σαφές περίγραμμα. Αντιλαμβανόμαστε το τι θα συνέβαινε, εάν ο στύλος είχε (περίπου) 15-πλάσιο ύψος, όσο αυτό της Πυραμίδος του Χέοπος (146,7μ).[/FONT]
[FONT=Times New Roman, serif]3η προϋπόθεση:[/FONT]
[FONT=Times New Roman, serif]Το έδαφος επί του οποίου ρίπτεται η σκιά της είναι τέλειο μαθηματικό επίπεδο, οριζόντιο.[/FONT]
–[FONT=Times New Roman, serif]Αυτό, προφανώς, δεν είναι αληθές. Εάν ο Θαλής ήθελε να το μετατρέψει (στοιχειωδώς) σε τέτοιο επίπεδο θα έπρεπε να διαστρώσει μία έκταση πολλών στρεμμάτων. (Οπότε δεν θα επρόκειτο περί της “μεθόδου της σκιάς” αλλά... περί της “μεθόδου της μπουλντόζας”.)[/FONT]
[FONT=Times New Roman, serif]4η προϋπόθεση:[/FONT]
[FONT=Times New Roman, serif]Η πυραμίς ήταν τέλεια, υπό την μαθηματική έννοια του όρου.[/FONT]
–[FONT=Times New Roman, serif]Αυτό δεν είναι αληθές. Όχι μόνον διότι η πυραμίς ήταν κτισμένη με ορθογώνιους ογκόλιθους, αλλά κυρίως, επειδή, κατά την εποχή του Θαλή ήταν, ήδη, 2000 ετών και, άρα, ήταν φθαρμένη (“ποντικοφαγωμένη”), προπάντων εις την κορυφή της.[/FONT]
[FONT=Times New Roman, serif]Εις τις φωτογραφίες που ακολουθούν (άνω και κάτω, λεπτομέρειες της μεσαίας), μπορούμε να διαπιστώσουμε το κατά πόσον, η πυραμίς, ομοιάζει προς μία μαθηματική.[/FONT]
[FONT=Times New Roman, serif]
[/FONT]
[FONT=Times New Roman, serif]Εν όσω κάποιοι αναγνώστες μπορεί να εξετάζουν το θέμα που ετέθη εις το τέλος του προηγουμένου μηνύματος, ήτοι, το [FONT=Times New Roman, serif]«π[/FONT]ότε συμβαίνει, η πυραμίς, να “ρίχνει” σκιά και πότε, όχι[FONT=Times New Roman, serif]»[/FONT], ας διατυπώσουμε τις υπόλοιπες τρεις προϋποθέσεις. Αυτές, θέτουν εν αμφιβόλω την όλη πεποίθηση ότι, ο Θαλής, χρησιμοποίησε την μέθοδο της σκιάς. Εν τούτοις, θα τις δεχθούμε διά τους λόγους που εξηγήσαμε, ήδη (εις το εν λόγω μήνυμα). Εκείνο που θα απορρίψουμε είναι το “σενάριο” ότι χρησιμοποίησε την σκιά του ύψους όταν, αυτή, ήταν κάθετη προς μία πλευρά της βάσεως της πυραμίδος. Θα αποδείξουμε ότι, κάτι τέτοιο, είναι [FONT=Times New Roman, serif]αντιφατικό ή/και παράλογο. Αυτό θα γίνει αφού έχουμε εξετάσει ικανοποιητικώς την, εν λόγω, κάθετη [/FONT]“ρίψη” της σκιάς[FONT=Times New Roman, serif] ([/FONT]εις το επόμενο μήνυμα[FONT=Times New Roman, serif])[/FONT].[/FONT]
[FONT=Times New Roman, serif][FONT=Times New Roman, serif]Ας συνεχίσουμε:[/FONT][/FONT]
[FONT=Times New Roman, serif]2α προϋπόθεση:[/FONT]
[FONT=Times New Roman, serif]Το φαινόμενο της περιθλάσεως του φωτός ...δεν συμβαίνει.[/FONT]
–[FONT=Times New Roman, serif]Ως προς το αν συμβαίνει αυτό, αρκεί μία απλή παρατήρηση: Εάν δούμε την σκιά που “ρίχνει” (π.χ.) ένας στύλος της ΔΕΗ, θα παρατηρήσουμε ότι καθώς αυτή απομακρύνεται από την βάση του στύλου, γίνεται όλο και πιο ασαφής, πιο “θαμπή”. Η δε σκιά της κορυφής του, δεν έχει κάποιο σαφές περίγραμμα. Αντιλαμβανόμαστε το τι θα συνέβαινε, εάν ο στύλος είχε (περίπου) 15-πλάσιο ύψος, όσο αυτό της Πυραμίδος του Χέοπος (146,7μ).[/FONT]
[FONT=Times New Roman, serif]3η προϋπόθεση:[/FONT]
[FONT=Times New Roman, serif]Το έδαφος επί του οποίου ρίπτεται η σκιά της είναι τέλειο μαθηματικό επίπεδο, οριζόντιο.[/FONT]
–[FONT=Times New Roman, serif]Αυτό, προφανώς, δεν είναι αληθές. Εάν ο Θαλής ήθελε να το μετατρέψει (στοιχειωδώς) σε τέτοιο επίπεδο θα έπρεπε να διαστρώσει μία έκταση πολλών στρεμμάτων. (Οπότε δεν θα επρόκειτο περί της “μεθόδου της σκιάς” αλλά... περί της “μεθόδου της μπουλντόζας”.)[/FONT]
[FONT=Times New Roman, serif]4η προϋπόθεση:[/FONT]
[FONT=Times New Roman, serif]Η πυραμίς ήταν τέλεια, υπό την μαθηματική έννοια του όρου.[/FONT]
–[FONT=Times New Roman, serif]Αυτό δεν είναι αληθές. Όχι μόνον διότι η πυραμίς ήταν κτισμένη με ορθογώνιους ογκόλιθους, αλλά κυρίως, επειδή, κατά την εποχή του Θαλή ήταν, ήδη, 2000 ετών και, άρα, ήταν φθαρμένη (“ποντικοφαγωμένη”), προπάντων εις την κορυφή της.[/FONT]
[FONT=Times New Roman, serif]Εις τις φωτογραφίες που ακολουθούν (άνω και κάτω, λεπτομέρειες της μεσαίας), μπορούμε να διαπιστώσουμε το κατά πόσον, η πυραμίς, ομοιάζει προς μία μαθηματική.[/FONT]
[FONT=Times New Roman, serif]
[/FONT]
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα

21-01-14

14:36
[FONT=Times New Roman, serif]Περαιτέρω εξέταση της 1ης προϋπόθεσης:[/FONT]
[FONT=Times New Roman, serif]Ας επανέλθουμε, τώρα, εις την 1η προϋπόθεση (βλέπε #4,) και ας δούμε διά ποίο διάστημα του έτους, κατά την μεσημβρίαν (οπότε οι ηλιακές ακτίνες προσπίπτουν καθέτως επί την ΑΒ), η πυραμίς, “ρίχνει” ορατή σκιά (δηλαδή, εκτός της βάσεως ΑΒΓΔ) προς Βορράν και, ποίο διάστημα, δεν “ρίχνει”. Δηλαδή, πότε, η βόρεια έδρα της δεν φωτίζεται από τον Ήλιο και, πότε, φωτίζεται, αντιστοίχως.[/FONT]
[FONT=Times New Roman, serif]Αυτό θα το πράξουμε διότι, συν τοις άλλοις, έχει γενικότερο εγκυκλοπαιδικό και επιστημονικό ενδιαφέρον.[/FONT]
[FONT=Times New Roman, serif]Παρένθεση:[/FONT]
[FONT=Times New Roman, serif]Περί των σκιών της πυραμίδος προς τα άλλα σημεία του ορίζοντος, παρατηρούμε:[/FONT]
[FONT=Times New Roman, serif]Λόγω της θέσεώς της (βόρειο ημισφαίριο) και τις κλίσεως των εδρών της (βλέπε σχήμα στο τέλος), ποτέ δεν “ρίχνει” σκιά, προς Νότον. Βεβαίως, πάντοτε “ρίχνει” σκιά προς Δυσμάς (το πρωΐ) και προς Ανατολάς (το απόγευμα) αλλά, αυτές οι σκιές, ποτέ δεν προκύπτουν από ηλιακές ακτίνες κάθετες προς τις πλευρές ΒΓ και ΔΑ της ΑΒΓΔ διότι, ο μεν Ήλιος “ανεβαίνει” προς Βορράν, μέχρι 23.45ο γεωγραφικού πλάτους, η δε πυραμίς είναι σε πλάτος 30ο. Οπότε, οι σκιές αυτές, εμπίπτουν εις την περίπτωση κατά την οποία (συμφώνως προς την “διάδοση”) «ο Θαλής δεν μπορεί να κάνει τίποτε», δηλαδή, δεν μπορεί να υπολογίσει την ΣΚ (βλέπε #1).[/FONT]
[FONT=Times New Roman, serif]Τέλος της παρένθεσης.[/FONT]
[FONT=Times New Roman, serif]Εάν κατά την διάρκεια ενός μεγάλου διαστήματος (μεγαλυτέρου του μισού έτους – όπως φαίνεται στο σχήμα) η βόρεια έδρα φωτίζεται την στιγμή της μεσημβρίας (άρα, δεν “ρίχνει” σκιά προς Βορράν), αυτό σημαίνει το εξής:[/FONT]
[FONT=Times New Roman, serif]Εάν ο Θαλής είχε αφιχθεί εις την Γκίζα κατά την διάρκεια του εν λόγω διαστήματος (ακόμη και κατά την ημέρα της ενάρξεώς του), θα έπρεπε να περιμένει την παρέλευσή του, προκειμένου να χρησιμοποιήσει την “μέθοδο της σκιάς”, κατά την στιγμή της μεσημβρίας... Αυτό είναι παράξενο για ένα άνθρωπο που ...δεν συνήθιζε να χάνει τον χρόνο του και αρκεί διά να απορρίψουμε την εν λόγω μέθοδο ως μη έχουσα ετήσια εφαρμογή. Αλλά, και αν ακόμη υποθέσουμε ότι, ο Θαλής, επεσκέφθη την Γκίζα κατά την διάρκεια του άλλου διαστήματος, ήτοι, κατά το καλοκαίρι (βλέπε σχήμα) και ότι – όπως ο ...Τζίτζικας του παραμυθιού – δεν εσκέφθη το τι θα γινόταν τον χειμώνα, πάλι θα την απέρριπτε: Θα την απέρριπτε κατά την εφαρμογή της. Αυτό, θα το δούμε εις το επόμενο μήνυμα. Προς το παρόν όμως, ας εξετάσουμε το ζήτημα, όπως έχει τεθεί:[/FONT]
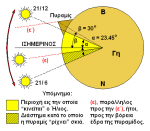
[FONT=Times New Roman, serif]Εις το σχήμα που ακολουθεί βλέπουμε την Γη από ένα σημείο της Ανατολής κατά την στιγμή που ο Ήλιος μεσουρανεί εις την περιοχή της Γκίζας, ήτοι, είναι μεσημβρία.[/FONT]
[FONT=Times New Roman, serif]Ανάλογα με την εποχή του έτους, ο Ήλιος, κατά την στιγμή της μεσημβρίας, ευρίσκεται σε διαφορετική γωνία ως προς το επίπεδο του Ισημερινού. Κατά τους μήνες του Καλοκαιριού ευρίσκεται βορειότερα του Ισημερινού και κατά τους μήνες του Χειμώνα, νοτιότερα.[/FONT]
[FONT=Times New Roman, serif]Καθώς, ημέρα προς ημέρα, το σημείο μεσουρανήσεως του Ηλίου “κινείται”, έρχεται κάποια ημέρα κατά την οποία το σημείο αυτό, “κινούμενο” προς Βορράν, ευρίσκεται σε τέτοια θέση ώστε οι ακτίνες του Ηλίου να είναι (κατά προσέγγισιν) παράλληλες προς την βόρεια έδρα της πυραμίδος, Από την ημέρα αυτή, μέχρι την ημέρα που θα ευρεθεί, πάλιν, εις την αυτήν θέσιν, “κινούμενο” προς Νότον, η βόρεια έδρα της πυραμίδος φωτίζεται και, άρα, δεν “ρίχνει” σκιά.[/FONT][FONT=Times New Roman, serif]
[/FONT]
[FONT=Times New Roman, serif]Ας επανέλθουμε, τώρα, εις την 1η προϋπόθεση (βλέπε #4,) και ας δούμε διά ποίο διάστημα του έτους, κατά την μεσημβρίαν (οπότε οι ηλιακές ακτίνες προσπίπτουν καθέτως επί την ΑΒ), η πυραμίς, “ρίχνει” ορατή σκιά (δηλαδή, εκτός της βάσεως ΑΒΓΔ) προς Βορράν και, ποίο διάστημα, δεν “ρίχνει”. Δηλαδή, πότε, η βόρεια έδρα της δεν φωτίζεται από τον Ήλιο και, πότε, φωτίζεται, αντιστοίχως.[/FONT]
[FONT=Times New Roman, serif]Αυτό θα το πράξουμε διότι, συν τοις άλλοις, έχει γενικότερο εγκυκλοπαιδικό και επιστημονικό ενδιαφέρον.[/FONT]
[FONT=Times New Roman, serif]Παρένθεση:[/FONT]
[FONT=Times New Roman, serif]Περί των σκιών της πυραμίδος προς τα άλλα σημεία του ορίζοντος, παρατηρούμε:[/FONT]
[FONT=Times New Roman, serif]Λόγω της θέσεώς της (βόρειο ημισφαίριο) και τις κλίσεως των εδρών της (βλέπε σχήμα στο τέλος), ποτέ δεν “ρίχνει” σκιά, προς Νότον. Βεβαίως, πάντοτε “ρίχνει” σκιά προς Δυσμάς (το πρωΐ) και προς Ανατολάς (το απόγευμα) αλλά, αυτές οι σκιές, ποτέ δεν προκύπτουν από ηλιακές ακτίνες κάθετες προς τις πλευρές ΒΓ και ΔΑ της ΑΒΓΔ διότι, ο μεν Ήλιος “ανεβαίνει” προς Βορράν, μέχρι 23.45ο γεωγραφικού πλάτους, η δε πυραμίς είναι σε πλάτος 30ο. Οπότε, οι σκιές αυτές, εμπίπτουν εις την περίπτωση κατά την οποία (συμφώνως προς την “διάδοση”) «ο Θαλής δεν μπορεί να κάνει τίποτε», δηλαδή, δεν μπορεί να υπολογίσει την ΣΚ (βλέπε #1).[/FONT]
[FONT=Times New Roman, serif]Τέλος της παρένθεσης.[/FONT]
[FONT=Times New Roman, serif]Εάν κατά την διάρκεια ενός μεγάλου διαστήματος (μεγαλυτέρου του μισού έτους – όπως φαίνεται στο σχήμα) η βόρεια έδρα φωτίζεται την στιγμή της μεσημβρίας (άρα, δεν “ρίχνει” σκιά προς Βορράν), αυτό σημαίνει το εξής:[/FONT]
[FONT=Times New Roman, serif]Εάν ο Θαλής είχε αφιχθεί εις την Γκίζα κατά την διάρκεια του εν λόγω διαστήματος (ακόμη και κατά την ημέρα της ενάρξεώς του), θα έπρεπε να περιμένει την παρέλευσή του, προκειμένου να χρησιμοποιήσει την “μέθοδο της σκιάς”, κατά την στιγμή της μεσημβρίας... Αυτό είναι παράξενο για ένα άνθρωπο που ...δεν συνήθιζε να χάνει τον χρόνο του και αρκεί διά να απορρίψουμε την εν λόγω μέθοδο ως μη έχουσα ετήσια εφαρμογή. Αλλά, και αν ακόμη υποθέσουμε ότι, ο Θαλής, επεσκέφθη την Γκίζα κατά την διάρκεια του άλλου διαστήματος, ήτοι, κατά το καλοκαίρι (βλέπε σχήμα) και ότι – όπως ο ...Τζίτζικας του παραμυθιού – δεν εσκέφθη το τι θα γινόταν τον χειμώνα, πάλι θα την απέρριπτε: Θα την απέρριπτε κατά την εφαρμογή της. Αυτό, θα το δούμε εις το επόμενο μήνυμα. Προς το παρόν όμως, ας εξετάσουμε το ζήτημα, όπως έχει τεθεί:[/FONT]
[FONT=Times New Roman, serif]Εις το σχήμα που ακολουθεί βλέπουμε την Γη από ένα σημείο της Ανατολής κατά την στιγμή που ο Ήλιος μεσουρανεί εις την περιοχή της Γκίζας, ήτοι, είναι μεσημβρία.[/FONT]
[FONT=Times New Roman, serif]Ανάλογα με την εποχή του έτους, ο Ήλιος, κατά την στιγμή της μεσημβρίας, ευρίσκεται σε διαφορετική γωνία ως προς το επίπεδο του Ισημερινού. Κατά τους μήνες του Καλοκαιριού ευρίσκεται βορειότερα του Ισημερινού και κατά τους μήνες του Χειμώνα, νοτιότερα.[/FONT]
[FONT=Times New Roman, serif]Καθώς, ημέρα προς ημέρα, το σημείο μεσουρανήσεως του Ηλίου “κινείται”, έρχεται κάποια ημέρα κατά την οποία το σημείο αυτό, “κινούμενο” προς Βορράν, ευρίσκεται σε τέτοια θέση ώστε οι ακτίνες του Ηλίου να είναι (κατά προσέγγισιν) παράλληλες προς την βόρεια έδρα της πυραμίδος, Από την ημέρα αυτή, μέχρι την ημέρα που θα ευρεθεί, πάλιν, εις την αυτήν θέσιν, “κινούμενο” προς Νότον, η βόρεια έδρα της πυραμίδος φωτίζεται και, άρα, δεν “ρίχνει” σκιά.[/FONT][FONT=Times New Roman, serif]
[/FONT]
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
Χρήστες Βρείτε παρόμοια
-
Φορτώνει...
 Αρχική Forum
Αρχική Forum
 Νέα Δημοσίευση
Νέα Δημοσίευση
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πολυμέσα - Gallery
Πολυμέσα - Gallery
 Chat
Chat
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 Chat and Fun
Chat and Fun iSchool
iSchool