Το ερωτικό τρίγωνο του πάθους

[Rempeskes]

Ο τίτλος είναι μούφα, για να προσελκύσω αναγνώστες.



...Σύμφωνα με την επίμονη γνώμη του μαθηματικού μου στο Γυμνάσιο, το άθροισμα των γωνιών ενός τριγώνου είναι ένα ακτίνιο π (180 μοίρες) - και τίποτα άλλο. Επειδή πάντα πίστευα ότι μου έλεγαν, με έκπληξη ανακάλυψα ότι τα πράγματα δεν είναι πάντοτε έτσι.

Βέβαια, έπρεπε πρώτα να πείσω τον εαυτό μου πως δεν είχε δίκιο...



(Φωνή της συνείδησης) - Εννοείς δηλαδή πως το άθροισμα των γωνιών δεν είναι π?

- Όχι. Εννοώ πως εξαρτάται από έναν βασικό παράγοντα: το αν καμπυλώνεται ο χώρος γύρω από το τρίγωνο.

(Φωνή της συνείδησης) - Καμπύλωση? Πως γίνεται αυτό να έχει σημασία?

- Γίνεται και παραγίνεται. Βλέπεις ο κόσμος δεν είναι επίπεδος, όπως το χαρτί πάνω στο οποίο ζωγραφίζεις τρίγωνα.

- Εξακολουθώ να είμαι δύσπιστος. Μπορείς να μου το αποδείξεις?

-- Πουρκουά πα? Εξάλλου, μπορεί να μάθεις και κάτι.
Έχεις ακουστά τον τύπο Γκάους-Μποννέ?

- Όχι, δεν τον έχω γνωρίσει.

- Ζώον, εννοώ τη φόρμουλα, την εξίσωση. Οπότε, δεν τη γνωρίζεις, και πάμε από την αρχή...

- Συγγνώμη. Συνέχισε...

- Από τις πάμπολλες περιπτώσεις καμπύλωσης μιας γεωμετρίας, θα εξετάσουμε κάποιες απλές περιπτώσεις: Τότε όταν η καμπυλότητα είναι σταθερή.

- Χμμμ... Παράδειγμα?

- Το Ευκλείδειο επίπεδο, έχει καμπυλότητα σταθερή και ίση με μηδέν. Αντίθετα, μια σφαίρα - όπως η επιφάνεια της Γης - έχει σταθερή θετική καμπυλότητα.

- Και στη περίπτωση που η καμπυλότητα είναι αρνητική?

- Εδώ χρειάζεται λίγο περισσότερη ενόραση. Μπορείς να φανταστείς μια τέτοια γεωμετρία ως εξής. Ας πούμε ότι είσαι στο δωμάτιο σου, και σηκώνεσαι να βγείς έξω. Όσο περπατάς προς την πόρτα όμως, ανακαλύπτεις με φόβο ότι συρρικνώνεσαι!
Συνεχίζεις με πείσμα να περπατάς προς την πόρτα, μα μικραίνεις όλο και περισσότερο - οπότε η απόσταση που πρέπει να διανύσεις σου φαίνεται να μεγαλώνει. Αυτή η γεωμετρία έχει αρνητική καμπυλότητα, και θα την αποκαλούμε επίπεδο Πουανκαρέ .

- Από τις φυλακές τους δεν θα δραπετεύει κανείς. Συνέχισε όμως. Κάτι έλεγες για έναν τύπο.

- Ναι, ο τύπος Γκάους-Μποννέ. Για να τον διατυπώσουμε, θεώρησε οποιαδήποτε από τις τρεις προηγούμενες γεωμετρίες, και ένα τρίγωνο Τ επί αυτής. Πες ότι οι πλευρές του τριγώνου έχουν την ιδιότητα να ελαχιστοποιούν τοπικά την απόσταση ανάμεσα στα σημεία τους - τότε οι πλευρές ονομάζονται "γεωδαιτικές", και αυτή η παραδοχή απλοποιεί τον τύπο. Πες επίσης ότι οι εσωτερικές γωνίες του Τ είναι α,β,γ. Τότε, ο τύπος Γκάους-Μποννέ αναφέρει ότι

και ελπίζω να μην σε τρομάζει ένα διπλό ολοκλήρωμα - λησμόνησα να σου αναφέρω ότι οι τρεις γεωμετρίες
που εξετάζουμε είναι διδιάστατες.

- Χμμμ... Ωραία. Και τι καταλαβαίνουμε από τον τύπο;

- Δεν καταλαβαίνουμε τίποτα αν δεν τον αξιοποιήσουμε. Ας πάμε για παράδειγμα στο Ευκλείδειο επίπεδο. Είπαμε ότι η καμπυλότητα είναι μηδέν. Αντικαθιστώντας Κ=0 στον προηγούμενο τύπο και έχουμε

όπως επέμενε ο μαθηματικός σου.

- Μάλιστα... Αν είμαστε στην επιφάνεια της Γης, τι συμβαίνει?

- Πάμε πάλι στον τύπο και αντικαθιστούμε Κ=1 (υποτιμώντας κομμάτι την ακτίνα της γης!). Τότε το διπλό ολοκλήρωμα γίνεται το εμβαδόν Ε του τριγώνου, και ο τύπος γίνεται

δηλαδή εδώ το άθροισμα των γωνιών είναι περισσότερο από π, και κατά πόσο περισσότερο εξαρτάται από το εμβαδόν του τριγώνου.

- Ε αυτό είναι πανζουρλισμός! Πως γίνεται μια γωνία να έχει τόσες πολλές μοίρες??

- Γίνεται και παραγίνεται, και είναι γνωστό στους χαρτογράφους πολύ πριν ανακαλυφθεί ο τύπος. Δες το ως εξής. Είσαι στον Βόρειο Πόλο και κατηφορίζεις τον μεσημβρινό προς το Πορτ-Ζεντίλ της Γκαμπόν. Κάθεσαι για ένα αναψυκτικό και κατευθύνεσαι κατα μήκος του Ισημερινού για το Ποντιανάκ της Ινδονησίας. Μόλις φτάσεις και εκεί, πετάς τα λιωμένα σου παπούτσια και ξεκινάς για τον Βόρειο Πόλο πάλι, κατά μήκος του μεσημβρινού.
Αφού έχεις ξεθεωθεί στο περπάτημα, γυρνάς και αθροίζεις τις γωνίες του τριγώνου: Σχεδόν 3π/2, ή 270 μοίρες.

- Προτιμώ να μείνω εδώ που κάθομαι και να τα δω στο γκούγκλ έρθ. Μη σε σταματάω όμως. Μας έχει μείνει το επίπεδο του Πουνκαρ, Πουαναρ...?

- Πουανκαρέ. Εδώ έχουμε χαριστικά Κ=-1, άρα ο τύπος γίνεται

δηλαδή το άθροισμα των γωνιών είναι λιγότερο από π.

- Να πω πως δεν το περίμενα...?
Μάλιστα. Μπορείς να μου δώσεις ένα παράδειγμα επί αυτού?

- Χμ. Θεώρησε πως τρεις ακτίνες φωτός εκπέπονται από το ίδιο σημείο στην επιφάνεια μια μαύρης τρύπας, αλλά δεν καταφέρνουν να ξεφύγουν από το βαρυτικό της πεδίο και εγκλωβίζονται ξανά μέσα της (αλλιώς, θα λεγόταν "φωτεινή τρύπα"). Αυτό το τρίγωνο, δεν το περιμένεις να έχει και το μεγαλύτερο εμβαδόν του κόσμου!

- Μπερδεύτηκα. Δύσκολα τα μαθηματικά γαμ*το...

- Αν σου άρεσαν τα εύκολα, να γινόσουν ΓΓ στο υπουργείο Πολιτισμού. Δεν σου είπα και το άλλο όμως...

- Τι? Έχει και άλλο?

- Αμέ. Τα πυθαγόρεια θεωρήματα.

- Ώπα, περίμενε. Το πυθαγόρειο είναι ένα θεώρημα!

- Χμμμ... Στη πραγματικότητα είναι τρία, ένα για κάθε γεωμετρία.

- Μα πως γίνεται αυτό? Ποιά γεωμετρία είναι λάθος?

- Λάθος, είπες? Καμμία! Ή ίσως και όλες, τώρα που το λες. Γιατί έχουν όλες τον ίδιο βαθμό πιστότητας - αν άυριο μια από αυτές καταρριφθεί επειδή παράγει παράδοξα, τότε όλες τους θα είναι για πέταμα.

- Αν είναι δυνατόν! Συμβαίνουν αυτά στην Βασίλισσα των Επιστημών?

- Και χειρότερα. Αλλά ας μην μπούμε σε αυτή τη κουβέντα. Σου χρωστάω δύο Πυθαγόρεια θεωρήματα, θα σου δώσω το ένα και σκάσε. Πες τα μήκη των πλευρών Α,Β, Γ.

Επί σφαίρας με ακτίνα R,

ισχύει

.

- Xα! Τι μπαρούφα είναι αυτή??? Αυτό δεν είναι το πυθαγόρειο! Με δουλεύεις τόση ώρα...

- Λες και το 'ξερα ότι θα διαφωνήσεις.
Δες το ως εξής. Αναπτύσσοντας το σφαιρικό πυθαγόρειο κατά Τέυλορ, έχουμε

Όταν λεπόν η ακτίνα R είναι κατά πολύ μεγαλύτερη από τις πλευρές, ξεχνάμε το 1/R στον τελευταίο τύπο, και καταλήγουμε στο -γνωστό και στον μαθηματικό σου - Πυθαγόρειο Θεώρημα.

- Μάλιστα... Τι να πει κανείς. Πάω να δω Πρίζον Μπρέηκ.

- Το μυαλό σου και μια λίρα. Έχεις τόσο εγκλιματιστεί στα σκουπίδια, που δεν μπορείς να διακρίνεις τίποτε άλλο.

- Λολ, γουατέβα. Σι γιου...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[fandago]

Αν το κείμενο είναι δικό σου, συγχαρητήρια. Πολύ ενδιαφέρον και ευχάριστο στο διάβασμα, καθώς και εποικοδομητικό.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kloyklos]

εγω τα παράτησα μετα την πρώτη πρόταση

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Kargas]

Αν το κείμενο είναι δικό σου, συγχαρητήρια. Πολύ ενδιαφέρον και ευχάριστο στο διάβασμα, καθώς και εποικοδομητικό.

+άπειρο

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Εδάδ]

A ρε Ρεμπεσκέ, μπήκα εδώ να διαβάσω τίποτα πικάντικο και το μόνο που βρήκα να πλησιάζει ήταν μια ολοκλήρωση (μαθηματική για να εξηγούμαστε βεβαίως-βεβαίως)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

Αν το κείμενο είναι δικό σου, συγχαρητήρια.

Για να πω την αληθεια, οφείλω μερικη από την έμπνευση μου στα μέρη 1+2 αυτής της σελίδας.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[roumana]

Rempeskes αν είχα δάσκαλο που να μου μάθει μαθηματικά με τόσο αστείο τρόπο είμαι σίγουρη ότι σήμερα θα ήξερα πολύ περισσότερα…

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

Δεν είχα αναφέρει και παραδείγματα τριγώνων, για κάθε μια γεωμετρία...

Για την γεωμετρία του Ρίμαν, θεωρήστε το τρίγωνο που παράγεται από δύο τυχαίους μεσημβρινούς και την καμπύλη της εικόνας:

Για τα τρίγωνα την Ευκλείδεια γεωμετρία, ανοίξτε τα σχολικά σας

...Κανείς δεν ανέφερε προηγουμένως ότι δεν έχω προσθέσει σχηματική αναπαράσταση για Υπερβολικό τρίγωνο.

Αυτό μου είχε σπάσει τα νεύρα για καιρό, δεν έβρισκα τίποτα ανάλογο.


...Μα κατάφερα επιτέλους να βρω πως θα έμοιαζε μια διδιάστατη προβολή ενός τρίγωνου με πλευρές από ακτίνες φωτός, που εκπέμπονται και παγιδεύονται στον ορίζοντα γεγονότων μιας μαύρης τρύπας.

Στην επόμενη εικόνα:

Εδώ ο ποπός χρησιμεύει ως ορίζοντας γεγονότων, ενώ οι άκρες του τάγκα είναι οι πλευρές του τριγώνου. Να ευχαριστήσουμε βεβαίως και το ευγενές σπορ της σανιδοπλοϊας, που προωθεί τις επιστήμες.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Skoulikadera---]

....αχ, αχ! πόσους φραπέδες είπιες πάλι σήμερα...?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

Tέσσερεις, οι δύο πρώτοι σκέτοι με έξι κουταλιές, και έχουμε ακόμα φως.

εδιτ: για να μη λες ότι έχω εθιστεί, σου λέω ότι ο καφές με βοηθά να ηρεμήσω, νυστάζω όταν πίνω.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Palladin]

αυτό το θρεντ εγώ τώρα το ανακάλυψα.
αρχικά υποκλίνομαι, ήταν εξαιρετικό
γράψε μας κι άλλα τέτοια πλιζ (κατά προτίμηση γράψε βιβλίο, θα βάλεις κάτω όλους τους καθηγηταράδες)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Tsipouro]

Πρώτα απ' όλα συγχαρητήρια για το καταπληκτικό topic. Το ανακάλυψα πριν λίγες μέρες αλλά δεν το κατάλαβα και τόσο καλά.

Απορίες:

Έχεις ακουστά τον τύπο Γκάους-Μποννέ?

Αυτόν τον τύπο όχι, δεν τον έχω ακουστά και επειδή θέλω να καταλάβω το topic, αν μπορείς γράψτον με latex και πόσταρέ τον plz.
(άκυρο, το βρήκα από αλλού)

Μπορείς να φανταστείς μια τέτοια γεωμετρία ως εξής. Ας πούμε ότι είσαι στο δωμάτιο σου, και σηκώνεσαι να βγείς έξω. Όσο περπατάς προς την πόρτα όμως, ανακαλύπτεις με φόβο ότι συρρικνώνεσαι!
Συνεχίζεις με πείσμα να περπατάς προς την πόρτα, μα μικραίνεις όλο και περισσότερο - οπότε η απόσταση που πρέπει να διανύσεις σου φαίνεται να μεγαλώνει.

Επειδή αυτό σαν Γεωμετρία είναι κομματάκι δύσκολο να το φανταστώ, μπορεί να εξηγηθεί με τους τύπους της σχετικής ταχύτητας. π.χ. ξεκινάς από μια θέση και σε αυτή τη θέση
υπάρχει ένας παρατηρητής που καθώς εσύ θα προχωράς προς την πόρτα αυτός θα μείνει ακίνητος σε εκείνο το σημείο και μπορεί μετρώντας την απόστασή σου από τη δική του θέση (παρατηρητής: Α, εσύ: Β, τύπος Χ(Α)=Χ(Α)+Χ(Β) αν υποθέσουμε ότι η κίνηση γίνεται σε ευθεία γραμμή);

lol, αυτό τώρα το 'νιωσα...

- Και χειρότερα. Αλλά ας μην μπούμε σε αυτή τη κουβέντα. Σου χρωστάω δύο Πυθαγόρεια θεωρήματα, θα σου δώσω το ένα και σκάσε. Πες τα μήκη των πλευρών Α,Β, Γ.

Επί σφαίρας με ακτίνα R,

ισχύει

.

- Xα! Τι μπαρούφα είναι αυτή??? Αυτό δεν είναι το πυθαγόρειο! Με δουλεύεις τόση ώρα...

- Λες και το 'ξερα ότι θα διαφωνήσεις.
Δες το ως εξής. Αναπτύσσοντας το σφαιρικό πυθαγόρειο κατά Τέυλορ, έχουμε

Όταν λεπόν η ακτίνα R είναι κατά πολύ μεγαλύτερη από τις πλευρές, ξεχνάμε το 1/R στον τελευταίο τύπο, και καταλήγουμε στο -γνωστό και στον μαθηματικό σου - Πυθαγόρειο Θεώρημα.

Εδώ στα κενά ανάμεσα στις προτάσεις θα έπρεπε να έχει τύπους και το ανάπτυγμα του σφαιρικού πυθαγορείου κατά Taylor που λες... Εγώ γιατί δεν τα βλέπω;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

Εδώ στα κενά ανάμεσα στις προτάσεις θα έπρεπε να έχει τύπους και το ανάπτυγμα του σφαιρικού πυθαγορείου κατά Taylor που λες... Εγώ γιατί δεν τα βλέπω;;;

Γιατί ο TeXer δεν είναι υποχρεωμένος να μου κάνει hosting εις τον αιώνα τον άπαντα
Πάντως αν είχες ΙΕ, θα έβλεπες το broken image και θα καταλάβαινες το σαμποτάζ.

μπορεί να εξηγηθεί με τους τύπους της σχετικής ταχύτητας

Δεν είναι θέμα παρατηρητή. Κανείς δε θα μπορούσε να σταθεί στη πόρτα, γιατί... δεν υπαρχει τίποτα εκεί. Είναι θέμα μήκους, ή αν θες, "μετρικής". Όσο πιο κοντά στη πόρτα, τόσο μεγαλύτερες οι αποστάσεις των γειτονικών σημείων.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Tsipouro]

Δεν είναι θέμα παρατηρητή. Κανείς δε θα μπορούσε να σταθεί στη πόρτα, γιατί... δεν υπαρχει τίποτα εκεί. Είναι θέμα μήκους, ή αν θες, "μετρικής". Όσο πιο κοντά στη πόρτα, τόσο μεγαλύτερες οι αποστάσεις των γειτονικών σημείων.

Thx. Μπορείς και να μου περιγράψεις συνοπτικά αυτή τη Γεωμετρία;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

Μπορείς να φανταστείς μια αρνητικά καμπυλωμένη γεωμετρία ως εξής. Στον μοναδιαίο δίσκο του μιγαδικού επιπέδου, ορίζουμε την απόσταση των σημείων z και w ως

​

Και τώρα, μια ρήξη με το κατεστημένο:
Το 5ο αίτημα του Ευκλείδη αναφέρει πως "Από σημείο εκτός ευθείας διέρχεται μοναδική παράλληλη σε αυτήν"(1)
Πάμε να το καταρρίψουμε?

Με το νέο τρόπο υπολογισμού των αποστάσεων, λαμβάνουμε αυτόματα πως οι γεωδαιτικές (δηλαδή, οι καμπύλες ελάχιστου μήκους) αποτελούνται απο καμπύλες όπως στην επόμενη εικόνα:

Κάθε μία από αυτές τις καμπύλες αποτελεί και μια "ευθεία" της υπερβολικής γεωμετρίας. Εύκολα βλέπουμε πως "Απο σημείο εκτός ευθείας, διέρχονται περισσότερες από μία παράλληλες σε αυτήν".

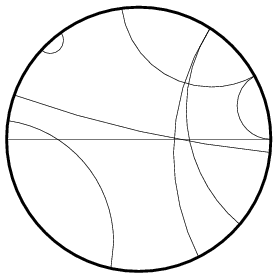
...Πόσες ακριβώς?





(1) Αυτή η μορφή του αιτήματος διατυπώθηκε δύο χιλιετίες μετά τον Ευκλείδη, από τον John Playfair.
​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[moonlight]

καταρχην υποκλεινομαι
τωρα που το θυμηθηκα κατι πολυ απλο για σας δασκαλε μου, μια φιλη μου μαθηματικος μου εξηγησε πως βρησκεις το εμβαδο μιας καρδιας... θα μπορουσατε να το παραθεσετε εδω ή καπου αλλου για να το θυμηθουμε??

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Idril]

Προφανώς εννοείς την καρδιοειδή καμπύλη: r = a(1-cosφ)

Πωπω τι μου θύμισες τώρα...Λογισμός 1, αξέχαστες στιγμές!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

μου εξηγησε πως βρησκεις το εμβαδο μιας καρδιας... θα μπορουσατε να το παραθεσετε εδω ή καπου αλλου για να το θυμηθουμε??

Εχμ, εμβαδόν καρδιάς; Για ποιό λόγο;
...Πρέπει να υπάρχει καλύτερος τρόπος για να δείς αν μια καρδιά σε χωράει

***

Προφανώς εννοείς την καρδιοειδή καμπύλη: r = a(1-cosφ)

Να που τελικά επαληθεύεται το κλισέ,
είτε θα είσαι καλός ερευνητής είτε καλός δάσκαλος
...Παραθέτοντας τύπους δεν απαντάς στο ερώτημα
​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[_Σταύρος_]

...Πρέπει να υπάρχει καλύτερος τρόπος για να δείς αν μια καρδιά σε χωράει

... δεν χωράς πια στην καρδιά μου, τα λάθη σου πολλά
μοναχός, μοναχός πιο καλά

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.