Guest 209912
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

09-04-21

22:08
Σε ένα σύστημα κρυπρογραφησης, καταγράψαμε ότι το κείμενο!Gl2Gδίνει"Jq9P. Ένας χρήστης εισάγει ένα password που κρυπτογραφείται σεid}7{. Ποιος ήταν ο κωδικός του?
i + 1
d + 3
} + 5
7 + 7
{ + 9
Οτι βγάζουν αυτά στο ascii table. Ο δημιουργός της συγκεκριμένης κρυπτογραφισης πρέπει να εκτελεσθεί.
WhaleOilBeefHooked
Νεοφερμένο μέλος
Ο WhaleOilBeefHooked αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 15 μηνύματα.

10-04-21

22:46
Σε καμία περίπτωση δεν είμουν εγώ ο δημιουργόςi + 1
d + 3
} + 5
7 + 7
{ + 9
Οτι βγάζουν αυτά στο ascii table. Ο δημιουργός της συγκεκριμένης κρυπτογραφισης πρέπει να εκτελεσθεί.
 Όχι ότι θα τη χρησιμοποιούσα ποτέ σε κάποιο πραγματκό σύστημα, είναι μόνο για την άσκηση.
Όχι ότι θα τη χρησιμοποιούσα ποτέ σε κάποιο πραγματκό σύστημα, είναι μόνο για την άσκηση.Για να την κλείνουμε, είναι περίπου όπως το είπες, η συνάρτηση αποκρυπτογράφησης είναι dec(x) = x - 2i - 1, όπου i ο δείκτης του χαρακτήρα x (από το 0). Από το ASCII table, ο κωδικός είναι hax0r.

16-06-21

23:48
Να σας πω ένα άλλο θέμα .
Η Nelliel μπορεί να λέει ας πούμε ότι βγήκε με 20 γκόμενους άρα είναι πιο πιθανό ο επόμενος γκόμενος να είναι καλός, αλλά θεωρητικά κάθε ραντεβού δεν είναι 50-50 να της αρέσει ή να μη της αρέσει ο άλλος ως ανεξάρτητο γεγονός κάθε φορά ; πως αθροίζεται αυτό σαν πιθανότητες και σκεφτόμαστε όλοι ότι η nelliel όταν θα βγει με 100 γκόμενους θα βρει τον καλό της ; ή είναι κάποιο σφάλμα της λογικής αυτό και στην ουσία με 1000 άντρες να βγούμε ή και οτιδήποτε που μπορεί να έχουμε στη ζωή μας έχουμε την ίδια πιθανότητα στην αποτυχία ;
Η Nelliel μπορεί να λέει ας πούμε ότι βγήκε με 20 γκόμενους άρα είναι πιο πιθανό ο επόμενος γκόμενος να είναι καλός, αλλά θεωρητικά κάθε ραντεβού δεν είναι 50-50 να της αρέσει ή να μη της αρέσει ο άλλος ως ανεξάρτητο γεγονός κάθε φορά ; πως αθροίζεται αυτό σαν πιθανότητες και σκεφτόμαστε όλοι ότι η nelliel όταν θα βγει με 100 γκόμενους θα βρει τον καλό της ; ή είναι κάποιο σφάλμα της λογικής αυτό και στην ουσία με 1000 άντρες να βγούμε ή και οτιδήποτε που μπορεί να έχουμε στη ζωή μας έχουμε την ίδια πιθανότητα στην αποτυχία ;
Guest 875331
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

17-06-21

01:41
Αν ήταν απόλυτα τυχαίο γεγονός, τότε το να πεις πως στο επόμενο ραντεβού έχεις παραπάνω πιθανότητες γτ τα προηγούμενα 50 ήταν αποτυχημένα αποτελεί το γνωστό gambler's fallacy. Αν εγώ ρίχνω ένα κέρμα και έρθει 10 φορές κορώνα τότε η πιθανότητα να έρθει κορώνα στην 11η είναι πάλι 50%. Στην πράξη όμως αυτά δεν έχουν καμία εφαρμογή στην πραγματική ζωή, ούτε καν στο χρηματιστήριο, οπότε δεν έχει νόημα να τα σκεφτόμαστε.Η Nelliel μπορεί να λέει ας πούμε ότι βγήκε με 20 γκόμενους άρα είναι πιο πιθανό ο επόμενος γκόμενος να είναι καλός, αλλά θεωρητικά κάθε ραντεβού δεν είναι 50-50 να της αρέσει ή να μη της αρέσει ο άλλος ως ανεξάρτητο γεγονός κάθε φορά ;
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, επαγγέλλεται Η.Μ.Μ.Υ. και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.734 μηνύματα.

17-06-21

03:21
Να σας πω ένα άλλο θέμα .
Η Nelliel μπορεί να λέει ας πούμε ότι βγήκε με 20 γκόμενους άρα είναι πιο πιθανό ο επόμενος γκόμενος να είναι καλός, αλλά θεωρητικά κάθε ραντεβού δεν είναι 50-50 να της αρέσει ή να μη της αρέσει ο άλλος ως ανεξάρτητο γεγονός κάθε φορά ; πως αθροίζεται αυτό σαν πιθανότητες και σκεφτόμαστε όλοι ότι η nelliel όταν θα βγει με 100 γκόμενους θα βρει τον καλό της ; ή είναι κάποιο σφάλμα της λογικής αυτό και στην ουσία με 1000 άντρες να βγούμε ή και οτιδήποτε που μπορεί να έχουμε στη ζωή μας έχουμε την ίδια πιθανότητα στην αποτυχία ;
Ακόμα και σε ένα τέτοιο ιδανικό σενάριο, θα αρκούσε να βγει με 10 γκόμενους για να της τύχει ένας καλός
 .Βέβαια ο Fast έχει δίκιο...αυτό είναι απλά θεωρία. Στην πράξη θα μπορούσε να τύχουν και 100 γκόμενοι σκάρτοι. Αλλά εαν με ρωτήσεις,όταν ήδη απο τις 10 δοκιμές βλέπεις οτι η πιθανότητα να μην πετύχεις έναν αγγίζει σχεδόν το 0, εε τότε you're missing the point
.Βέβαια ο Fast έχει δίκιο...αυτό είναι απλά θεωρία. Στην πράξη θα μπορούσε να τύχουν και 100 γκόμενοι σκάρτοι. Αλλά εαν με ρωτήσεις,όταν ήδη απο τις 10 δοκιμές βλέπεις οτι η πιθανότητα να μην πετύχεις έναν αγγίζει σχεδόν το 0, εε τότε you're missing the point  .
.Είναι σαν το infinite monkey theorem. Που λέει οτι εαν αφήσεις μια μαιμού να χτυπάει πλήκτρα στην τύχη για άπειρο χρόνο,τότε θα καταφέρει να γράψει οποιοδήποτε κείμενο είναι δυνατό(όπως ας πούμε ένα υπαρκτό βιβλίο), άπειρες φορές. Θεωρητικά γίνεται ναι...αλλά στην πράξη δεν νομίζω οτι υπάρχει μαιμού που θα μπορούσε να κάνει δοκιμές για άπειρο χρόνο .
Guest 209912
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

17-06-21

07:02
Να σας πω ένα άλλο θέμα .
Η Nelliel μπορεί να λέει ας πούμε ότι βγήκε με 20 γκόμενους άρα είναι πιο πιθανό ο επόμενος γκόμενος να είναι καλός, αλλά θεωρητικά κάθε ραντεβού δεν είναι 50-50 να της αρέσει ή να μη της αρέσει ο άλλος ως ανεξάρτητο γεγονός κάθε φορά ; πως αθροίζεται αυτό σαν πιθανότητες και σκεφτόμαστε όλοι ότι η nelliel όταν θα βγει με 100 γκόμενους θα βρει τον καλό της ; ή είναι κάποιο σφάλμα της λογικής αυτό και στην ουσία με 1000 άντρες να βγούμε ή και οτιδήποτε που μπορεί να έχουμε στη ζωή μας έχουμε την ίδια πιθανότητα στην αποτυχία ;
Το λογικό ΚΑΙ στις πιθανότητες είναι ο πολλαπλασιασμός.
Έστω ότι κάθε ραντεβού της Nelliel έχει 0.5 πιθανότητα επιτυχίας και είναι εντελώς ανεξάρτητο από τα υπόλοιπα.
Αν η Nelliel βγει 10 ραντεβού η πιθανότητα να μην βρει γκόμενο είναι η πιθανότητα να μην βρει στο πρώτο ΚΑΙ να μην βρει στο δεύτερο ΚΑΙ να μην βρει στο τρίτο κ.ο.κ.
Δηλαδή: Έστω Α η πιθανότητα να βρει γκόμενο σε ένα ραντεβού και Χ η πιθανότητα να μην βρει.
Α = Χ = 0.5Η πιθανότητα να βγει 10 ραντεβού και να μην βρει γκόμενο είναι:
Χ & Χ & Χ & Χ & Χ & Χ & Χ & Χ & Χ & Χ = 0.5^10 = 0.0009765625 δηλαδή μία στις δέκα χιλιάδες.Η πιθανότητα να βγει 10 ραντεβού και να βρει ΤΟΥΛΑΧΙΣΤΟ ένα γκόμενο θα ήταν η συμπληρωματική της παραπάνω πιθανότητας δηλαδή
1 - 0.0009765625 = 0.9990234375 δηλαδή σχεδόν σίγουρο.bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και επαγγέλλεται Σύμβουλος επιχειρήσεων. Έχει γράψει 344 μηνύματα.

17-06-21

13:26
Αν μας ενδιαφέρει να βρούμε πόσα επιτυχημένα ραντεβού θα έχει από n συνολικά ραντεβού η πιθανότητα δίνεται ως  = \binom{n}{x}p^x(1-p)^{n-x}) όπου X το πλήθος των επιτυχημένων ραντεβού και p η πιθανότητα επιτυχίας κάθε ραντεβού. Ο μέσος αριθμός θα είναι
όπου X το πλήθος των επιτυχημένων ραντεβού και p η πιθανότητα επιτυχίας κάθε ραντεβού. Ο μέσος αριθμός θα είναι =np)
Αν μας ενδιαφέρει να βρούμε πόσα αποτυχημένα ραντεβού θα έχει μέχρι να έχει r επιτυχημένα ραντεβού η πιθανότητα δίνεται ως = \binom{r-1+y}{r-1}p^r(1-p)^y) όπου Y το πλήθος των αποτυχημένων ραντεβού και το p ίδιο με πριν. Ισοδύναμα μπορούμε να μετρήσουμε πόσα συνολικά ραντεβού (Χ) χρειάζονται μέχρι r επιτυχίες που δίνεται από
όπου Y το πλήθος των αποτυχημένων ραντεβού και το p ίδιο με πριν. Ισοδύναμα μπορούμε να μετρήσουμε πόσα συνολικά ραντεβού (Χ) χρειάζονται μέχρι r επιτυχίες που δίνεται από = \binom{x-1}{r-1}p^r(1-p)^{x-r}) . Οι μέσοι αριθμοί θα είναι
. Οι μέσοι αριθμοί θα είναι =\frac{r(1-p)}{p}) ή
ή =\frac{r}{p}) .
.
Κάποιος θα πει όμως γιατί να είναι σταθερό το p; Εκεί πρέπει να σκεφτούμε με ένα μπεϋζιανό τρόπο. Μια πρότερη κατανομή Βήτα(α,β) για το P και μια δυωνυμική πιθανοφάνεια δεσμευμένη πάνω στο P θα ήταν μία εύλογη αρχή.
Οκ πρέπει να βρω γκόμενα.
Αν μας ενδιαφέρει να βρούμε πόσα αποτυχημένα ραντεβού θα έχει μέχρι να έχει r επιτυχημένα ραντεβού η πιθανότητα δίνεται ως
Κάποιος θα πει όμως γιατί να είναι σταθερό το p; Εκεί πρέπει να σκεφτούμε με ένα μπεϋζιανό τρόπο. Μια πρότερη κατανομή Βήτα(α,β) για το P και μια δυωνυμική πιθανοφάνεια δεσμευμένη πάνω στο P θα ήταν μία εύλογη αρχή.
Οκ πρέπει να βρω γκόμενα.
Paragontas7000
Περιβόητο μέλος
Ο Paragontas7000 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 22 ετών. Έχει γράψει 5.773 μηνύματα.

17-06-21

13:33
ΝαιΑν μας ενδιαφέρει να βρούμε πόσα επιτυχημένα ραντεβού θα έχει από n συνολικά ραντεβού η πιθανότητα δίνεται ωςόπου X το πλήθος των επιτυχημένων ραντεβού και p η πιθανότητα επιτυχίας κάθε ραντεβού. Ο μέσος αριθμός θα είναι
Αν μας ενδιαφέρει να βρούμε πόσα αποτυχημένα ραντεβού θα έχει μέχρι να έχει r επιτυχημένα ραντεβού η πιθανότητα δίνεται ωςόπου Y το πλήθος των αποτυχημένων ραντεβού και το p ίδιο με πριν. Ισοδύναμα μπορούμε να μετρήσουμε πόσα συνολικά ραντεβού (Χ) χρειάζονται μέχρι r επιτυχίες που δίνεται από
. Οι μέσοι αριθμοί θα είναι
ή
.
Κάποιος θα πει όμως γιατί να είναι σταθερό το p; Εκεί πρέπει να σκεφτούμε με ένα μπεϋζιανό τρόπο. Μια πρότερη κατανομή Βήτα(α,β) για το P και μια δυωνυμική πιθανοφάνεια δεσμευμένη πάνω στο P θα ήταν μία εύλογη αρχή.
Οκ πρέπει να βρω γκόμενα.
Μάξιμος
Διάσημο μέλος
Ο Μάξιμος αυτή τη στιγμή δεν είναι συνδεδεμένος. Επαγγέλλεται Σκηνοθέτης. Έχει γράψει 3.804 μηνύματα.

17-06-21

16:05
Πρέπει. Αλλά, να ξέρεις πως μία πανάρχαια μέθοδος ήταν αλάνθαστη.Αν μας ενδιαφέρει να βρούμε πόσα επιτυχημένα ραντεβού θα έχει από n συνολικά ραντεβού η πιθανότητα δίνεται ωςόπου X το πλήθος των επιτυχημένων ραντεβού και p η πιθανότητα επιτυχίας κάθε ραντεβού. Ο μέσος αριθμός θα είναι
Αν μας ενδιαφέρει να βρούμε πόσα αποτυχημένα ραντεβού θα έχει μέχρι να έχει r επιτυχημένα ραντεβού η πιθανότητα δίνεται ωςόπου Y το πλήθος των αποτυχημένων ραντεβού και το p ίδιο με πριν. Ισοδύναμα μπορούμε να μετρήσουμε πόσα συνολικά ραντεβού (Χ) χρειάζονται μέχρι r επιτυχίες που δίνεται από
. Οι μέσοι αριθμοί θα είναι
ή
.
Κάποιος θα πει όμως γιατί να είναι σταθερό το p; Εκεί πρέπει να σκεφτούμε με ένα μπεϋζιανό τρόπο. Μια πρότερη κατανομή Βήτα(α,β) για το P και μια δυωνυμική πιθανοφάνεια δεσμευμένη πάνω στο P θα ήταν μία εύλογη αρχή.
Οκ πρέπει να βρω γκόμενα.
Αυτή δεν είχε παραμέτρους.
Ηταν αποτελεσματικότατη.
Ενα ρόπαλο και με την μία και καλουπολογισμένη, έδινε μερική αμνησία.
Σταδιακά, επανέρχονταν, αλλά είχε καλομάθει στην Νέα Κανονικότητα και έτσι δεν υπήρχε κίνδυνος να το βάλει στα πόδια και να φύγει.
Οχι, βρες μου εσύ αποτελεσματικότερη μέθοδο...





Εν τάξε, αν είναι ερωτευμένη με εσένα, αυτό είναι εκτός συναγωνισμού.


17-06-21

16:13
Με ρόζους ή χωρίς ;Ενα ρόπαλο
Μάξιμος
Διάσημο μέλος
Ο Μάξιμος αυτή τη στιγμή δεν είναι συνδεδεμένος. Επαγγέλλεται Σκηνοθέτης. Έχει γράψει 3.804 μηνύματα.

17-06-21

16:24
Το μέγεθος στους ρόζους, είναι το λεπτό σημείο που χρήζει σωστών υπολογισμών.Με ρόζους ή χωρίς ;
Εξαρτάται, απο τα μαλλιά της γυναίκας, απο τη δυναμική του μυαλλού της (απαραίτητη προϋπόθεση να διαθέτει, υπάρχουν αμφιβολίες βάσιμες σε αυτό το σημείο).

Επίσης και αυτός που το κρατάει παίζει ρόλο βασικό.
Αν είναι ανίδεος, είναι και εξαιρετικά επικίνδυνος.
Θέλει αγαπησιάρικο υπολογισμό.

Για παράδειγμα, μόλις την δει, μπορεί να αρχίσουν πουλάκια να του κελαηδούν.
Να δεις για πότε γίνεται γατούλης...



Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

25-09-22

14:06
Ένα προβληματάκι που λύγισε το Mathway και το Microsoft Mathematics:
Βρείτε το όριο:
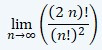
Βρείτε το όριο:
cannot_log_in
Νεοφερμένο μέλος
Ο cannot_log_in αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 9 μηνύματα.

11-11-23

13:25
Ένα προβληματάκι που λύγισε το Mathway και το Microsoft Mathematics:
Βρείτε το όριο:
View attachment 109061
Απειρίζεται.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 83 μέλη διάβασαν αυτό το θέμα:
- JohnnyW
- johnsala
- touvlo
- Εριφύλη
- Scandal
- cannot_log_in
- kalhkardia
- arko
- charitos
- fourkaki
- American Economist
- camil
- charmander
- Memetchi
- WhaleOilBeefHooked
- chester20080
- giannhs2001
- Paragontas7000
- Athens2002
- Viedo
- iminspain
- Freya Goddes
- harry akritas
- taketrance
- Libertus
- leo41
- orchidea
- Στεφανος56
- nucomer
- Εχέμυθη
- T C
- louminis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Νέα Δημοσίευση
Νέα Δημοσίευση
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πολυμέσα - Gallery
Πολυμέσα - Gallery
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 Chat and Fun
Chat and Fun iSchool
iSchool

