Φυσική vs Μαθηματικά

[ΜΠΕΡΔΕΜΕΝΟΣ]

η φυσική μου είναι πιο εύκολη στην κατανόηση

Ο Einstein είχε πει ότι τη θεωρία της σχετικότητας μόνο 2 άνθρωποι την έχουν κατανοήσει και ότι ο ίδιος δεν είναι ο ένας


Στο πνεύμα του ποστ σου (αλλά κ σε αντιδιαστολή με το "δεν πιστεύω αν δεν δω" των φυσικών):

"Το βλέπω αλλά δεν το πιστεύω" (Cantor (μαθηματικός), μάλλον για τις ανακαλύψεις του σχετικά με τα διαφορετικά είδη απείρου).

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Tsipouro]

Αριθμητική Γραμμική Άλγεβρα λέμε!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kalypso]

Ο Einstein είχε πει ότι τη θεωρία της σχετικότητας μόνο 2 άνθρωποι την έχουν κατανοήσει και ότι ο ίδιος δεν είναι ο ένας

Είπα το αντίθετο;

πς. Έχω έναν τελείως χαοτικό τρόπο σκέψης- ρώτα και τους συμφοιτητές μου
(Δεν) καταλαβαίνω τα πιο τρελά πράγματα που σε κάνουν να τραβάς τα μαλλιά σου, μα επειδή τα αντιλαμβάνομαι με έναν δικό μου τρόπο εντελώς κουλό , στο τέλος τα "αποκρυπτογραφώ" :X

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[liberator]

Σιγουρα η πρωταρχικη επιστιμη ηταν η φυσικη. Δεν νομιζω οι αρχαιοι ανθρωποι να ξυπνησαν μια μερα και να αρχισαν να βγαζουν μαθηματικα. Σκοπος τους ηταν να κατανοησουν τον κοσμο για να "φανε" καλυτερα κ πιο ευκολα.
Τα μαθηματικα χωρις τη φυσικη δεν εχουν ουσια. Οπως και η φυσικη χωρις τα μαθηματικα δεν κανει τιποτα.
Οσο αναφορα αυτα που λεει η κλεφτρα εχω να πω οτι τα μαθηματικα απο μονα τους δεν βοηθανε πουθενα. Δεν μπορω να καταλαβω πως βοηθανε τα μαθηματικα στην ιατρικη χωρις φυσικη και χημεια.........(πες μου ενα παραδειγμα).

Επισης δεν πιστευω πως τα μαθηματικα δεν ασχολουνται με πειραματα. Σιγουρα το 1+1=2 βασιστηκε σε πειραμα.
Ενας φυσικος παντα ξερει μαθηματικα ενω ενας μαθηματικος δεν ξερει απαραιτητα φυσικη. Αυτο δεν σημαινει πως τα μαθηματικα ειναι ανωτερα η οτι μπορουν να στεκουν χωρις τη φυσικη. αυτο διχνει οτι αυτοι οι μαθηματικοι δεν ξερουν για πιο λογο υπαρχουν. Υπαρχουν για να εξηγουν και να σιγουρευουν αυτα που λενε οι "ουσιαστικες" επιστημες. αυτο ειναι το πιο δυσκολο που υπαρχει. οχι να το παρατηρεις και να το καταγραφεις αλλα να το αποδεικνυεις.



Υ.Γ μια ερωτηση για τους μαθηματικους......επειδη λενε οτι τα μαθηματικα ειναι η απολυτη αληθεια...... Εχετε σκεφτει ποτε αν 1+1=3 ? (καταλαβαινετε τι εννοω)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

μια ερωτηση για τους μαθηματικους......επειδη λενε οτι τα μαθηματικα ειναι η απολυτη αληθεια

Και εσύ γιατί τους πιστεύεις;

Φυσική εναντίον Μαθηματικών

Βρίσκω την αντιπαράθεση ανούσια.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[wizardcia]

Έχω διαβάσει οτι ο ''Θεός'' πριν φτιάξει την γη, έλυνε μαθηματικά...
Γιαυτό θα πώ κατ επιλογήν οτι τα μαθηματικα ειναι ποιο όμορφα.
Δέν λεω οτι η φυσική ειναι χειρότερή αλλα οτι σαν μάθημα και ώς ενασχόλησή ειναι πολύ ποιο όμορφα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[epote]

καλα, εγω δεν ξερω ΚΑΝΕΝΑ *καλο* φυσικο που να μην ειναι ΕΞΑΙΡΕΤΙΚΟΣ μαθηματικος και δεν ξερω ΚΑΝΕΝΑ *καλο* μαθηματικο που να μην ειναι ΕΞΑΙΡΕΤΙΚΟΣ φυσικος.

be that as it may η φυσικη ειναι "υποσυνολο" του φορμαλισμου των μαθηματικων (υπαρχουν μαθηματικα που δεν εχουν φυσικες εφαρμογες), τι σημαινει ακριβως αυτο ομως? Τιποτα βασικα...

point is τα μαθηματικα ειναι για τη φυσικη ενα εργαλειο, απο την αλλη η φυσικη ειναι μια ερμηνια των μαθηματικων που βρισκεται η "κοντρα"?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[geomatical04]

Η διαφορά μεταξύ φυσικής και μαθηματικών είναι ίδια με τη διαφορά μεταξύ αυνανισμού και πραγματικού σεξ !

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[epote]

Eιμαι 100% σιγουρος οτι οι θεσεις σαν του liberator προερχονται απο ανθρωπους που δεν ξερουν ΟΥΤΕ μαθηματικα ΟΥΤΕ φυσικη.

Liberator βρες μου εναν μαθηματικο που να μην ξερει εξαιρετικη φυσικη σε παρακαλω.

Δεν μπορει να υπαρξει διαχωρισμος, η φυσικη ειναι μαθηματικα, δεν υπαρχει φυσικη χωρις μαθηματικα. Απο την αλλη η φυσικη ειναι το ΝΟΗΜΑ των μαθηματικων. Τα μαθηματικα δεν εχουν νοημα χωρις τη φυσικη.

(Αν και τωρα τελευταια τιποτα απο τα δυο δεν εχει νοημα - βλεπε υπερχορδες)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[geomatical04]

Το θέμα είναι να λύνεις μαθηματικά και να υπάρχει κάποιο νόημα... Όχι απλώς να σου αρέσει να ασχολείσαι με τεχνάσματα των αριθμών (του στίλ τι θα γινόταν αν 1=2 και 2=1) και περίεργες γεωμετρίες (σύμφωνα με τις οποίες ο κύκλος είναι ευθεία) χώρις να σε ενδιαφέρει τι σημαίνουν αυτα στον πραγματικό κόσμο.
Άλλωστε μην ξεχνάμε ότι ο διαφορικός λογισμός που είναι από τους κύριους λίθους των μαθηματικών ανακαλύφθηκε από τον Ισάκ Νέυτωνα ο οποίος ασχολούνταν με την ερμηνεία όρων της κλασικής μηχανικής και όχι με ανύπαρκτους γρίφους...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[epote]

geomatical: ειμαι σιγουρος οτι δεν εχεις ιδεα σε τι αναφερεσαι.

χιλλια συγνωμη που δειχνω ετσι επιθετικος, δεν το λεω με κακια, αλλα πραγματικα δεν εχεις ιδεα...

ο διαφορικος λογισμος ανακαλυφθηκε απο τον newton ΚΑΙ τον leibniz ταυτοχρονα. Εξελιξαν την φυσικη και εξελιχθηκαν ΑΠΟ τη φυσικη.

απο την αλλη η διαφορικη γεωμετρια (που ΔΕΝ λεει οτι ο κυκλος ειναι ευθεια αυτο δεν το λεει τιποτα και πουθενα για προφανης λογους...) ανακαλυφθηκε ως ενα καθαρα μαθηματικο δημιουργημα απο τoυς eyler, riemman κτλ

ε και 100 χρονια μετα την χρησημοποιησε ο αινσταιν για να φτιαξει μια θεωριουλα του...

απο την αλλη μεχρι τη δεκαετια του 50 η συναρτησιακη αναλυση δεν ειχε καμια εφαρμογη, τοτε την ανακαλυψαν οι κβαντομηχανικοι...

η θεωρια καπα (ενας κλαδος της αλγεβρικης τοπολογιας) μεχρι πριν 10 χρονια ηταν ενας τελειως αποκομενος και θεωριτικος κλαδος των μαθηματικων. Τωρα σιγα σιγα μπαινει στη φυσικη.

τα μαθηματικα ΕΧΟΥΝ νοημα να γινονται ως ασκησεις φορμαλισμου. Γιατι...ε...ποτε δεν ξερεις

η βαση των μαθηματικων (συνολοθεωρια) δεν εχει καμια πρακτικη εφαρμογη η ερμηνια.

σκεψου ομως να μην υπηρχε

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[geomatical04]

1) Ο Newton αυτό που έκανε ήταν να περιγράψει τους νόμους της κίνησης και... παρέπιπτόντως εξέληξε τα μαθηματικά προσφέροντας τους ένα εργαλείο που χρησιμοποίησε δηλ το διαφορικό διαφορικό λογισμό (Δηλαδή δεν έψαχνε αυτόν). Ακόμα Νεύτωνας ανακάλυψε παραγώγους, ολοκληρώματα κτλπ πολύ πρίν από τον Leibniz.

2) Εγώ δεν είπα ότι αυτά που ψάχνουν οι μαθηματικοί δεν έχουν νόημα επειδή δεν έχουν χρήση αλλά είναι ανύπαρκτα. Πχ. ένας φυσικός ψάχνει για την παράγωγο της θέσης ως προς τον χρόνο για να βρεί την ταχύτητα κάθε στιγμή που κινέιται ένα αυτοκίνητο. Ταυτόχρονα ένας μαθηματικός ψάχνει την παράγωγο f'( χ) (τι είναι το χ,f; τρώγεται αυτό)
​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[epote]

Και παλι συγνωμη αλλα δεν εχεις ιδεα πως γινεται η ερευνα στα μαθηματικα

Αυτο νομιζεις οτι κανει ενας μαθηματικος? ψαχνει μια παραγωγο? Τα μαθηματικα δεν ειναι ασκησουλες λυκειου, ειναι η μελετη και η ερευνα δομων, εσωτερικων σχεσεων και συμετριας.

Τι παει να πει ειναι "ανυπαρκτα"? Εσυ εχεις δει ποτε κανενα κουαρκ?

Τα μαθηματικα ειναι μια γλωσσα, ειναι η αλφαβητος της φυσης.

Και ο φυσικο δεν θα μπορουσε να εχει υπολογισμους για θεσεις και ταχυτητες αν δεν υπηρχε ο ΦΟΡΜΑΛΙΣΜΟΣ της παραγωγου, η παραγωγος ειναι ενα θεωρητικο πλαισιο κανονων που ΔΕΝ υπαρχει.

Οσες φορες εχουν γινει ανακαλυψεις στα μαθηματικα λογο αναγκης (να περιγραφει καποιο φαινομενο) αλλες τοσες εχουν γινει στη φυσικη λογο εξελιξης των μαθηματικων.

Ειναι απιστευτα βλακωδες να λεμε "η φυσικη εχει νοημα τα μαθηματικα δεν εχουν" γιατι η φυσικη ΕΙΝΑΙ μαθηματικα και τα μαθηματικα ΕΙΝΑΙ φυσικη.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rempeskes]

τα μαθηματικα ΕΙΝΑΙ φυσικη.

Δεν είμαι τόσο σίγουρος.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[epote]

(σουτ ρε, μην μας "δινεις" :p)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[geomatical04]

Εσυ εχεις δει ποτε κανενα κουαρκ?

Όχι αυτά τα πράγματα τα κάνουν σε μεγαλύτερα εργαστήρια. Ωστόσω έχω ανιχνεύσει αντιηλεκτρόνια που είναι λίγο μεγαλύτερα από τα κουαρκς. Εσύ έχεις δεί ποτέ μεταβλητή χ; Και εδώ είναι η διαφορά μας. (Δε μιλάω για εσένα προσωπικά. Φιλοσοφικά το θέτω)

Ο φυσικός δεν μιλάει για παράγωγο του χ,ψ,ζ αλλά συνήθως για ρυθμό που μεταβάλεται μιας ποσότητα.

Προφανώς και η έρευνα στα μαθηματικά δεν εστιάζεται στις παραγώγους όπως και η έρευνα στη φυσική δεν εστιάζεται στην κινηματική απλώς χρησιμοποιώ τις παραγώγους για να καταλαβαινόμαστε όλοι.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Scandal]

Για να μιλήσουμε και επιστημονικά
Τα Μαθηματικά ανήκουν στις ιδεατές - τυπολογικές επιστήμες και αποτελούν ένα σύστημα σκέψης. Από την άλλη, η Φυσική ανήκει στις εμπειρικές - ρεαλιστικές επιστήμες και απ' ότι φαίνεται χρησιμοποιεί τόσο το σύστημα σκέψης των Μαθηματικών όσο και το σύστημα αξιών και κανονισμών της Νομικής.



-petros

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Tsipouro]

@geomatical: Είναι σαν να λες ότι οι μαθηματικοί ερευνούν απλά για να ερευνούν, ενώ οι φυσικοί ερευνούν για κάποιον λόγο (ο οποίος είναι η κατανόηση και η εξήγηση της λειτουργίας των φυσικών μοντέλων).

Έχεις σκεφτεί όμως ότι όλα τα μαθηματικά, ακόμα και τα πιο αφηρημένα/"θεωρητικά" έχουν πρακτικές εφαρμογές;

π.χ.:
Για να απεικονίσουν τις σχέσεις μεταξύ συνόλων οι μαθηματικοί χρησιμοποίησαν γραφήματα:

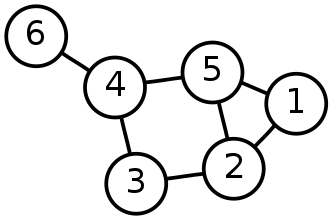
Ο euler σκέφτηκε να χρησιμοποιήσει τα γραφήματα σε εφαρμογές του πραγματικού κόσμου, π.χ. στο αν κάποιος μπορεί να περάσει μόνο μια φορά σε έναν περίπατο όλες τις γέφυρες του ποταμού Pregel.

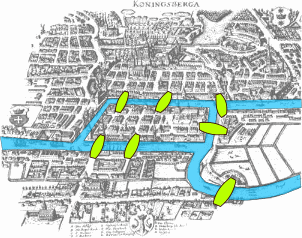
Σήμερα τα γραφήματα χρησιμοποιούνται στην πληροφορική για τη μελέτη της επιλυσιμότητας προβλημάτων και την ανάπτυξη δομών δεδομένων, στη χημεία και αλλού.
Δηλαδή, ένας καθαρά "θεωρητικός" στην αρχή του κλάδος των Μαθηματικών βρήκε εφαρμογή στην επίλυση προβλημάτων από πολλούς επιστημονικούς χώρους.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[thanosmylo]

Αυτό το θέμα είναι περίεργο και έχω δώει αρκετές απαντήσεις. Και θα δώσω μία ακόμα καθώς το συζήτησα με τον μαθηματικό μου στο φροντιστήριο.
Αυτός έχει τρέλα με τα μαθηματικά, δεν έγινε μόνο μαθηματικ΄ςο για να διδάξει αλλά αχολείται και μόνος του.

Ε και του κάνω πο πο, παντού εφαρμογές έχουν τα μαθηματικά.Όπου και αν σκεφτείς...χρειάζονται μαθηματικά.

Και μου λέει πως όντως η βάση των περισσότερων επιστημών είναι τα μαθηματικά, αλλά είναι η βάση. Και μου λέει για να τα εφαρμόσεις θα πρέπει να κάνεις άλλη επιστήμη. Π.χ. Φυσική, Οικονομικά, Χημεία

Με άλλα λόγια ναι μεν τα μαθηματικά είναι η βάση πολλών επιστημών, αλλά πρακτικά δεν είναι εφαρμόσιμα. Δηλαδή πρέπει να ασχοληθε΄ςι με άλλη επιστήμη για να τα εφαρμόσεις. Π.χ. Φυσική, π.χ. στην Οικονομία όπου εκεί εφαρμόζονται.

Και είναι σωστό, στη φυσκή τα εφαρμόζεις και αναλύεις ένα φαινόμενο ή στα οικονομικά τα εφαρμόζεις και βγάζεις συμπεράσματα για τα οικονομικά.

Εξάλλου όπου πας να εφαρμόσεις μαθηματικά για να βρεις κάτι μεταβαίνεις στα χωράφια άλλης επιστήμης. Πας να βρεις με μαθηματικά ένα φαινόμενο = ΦΥσική
Πας με μαθηματικά να αναλύσεις τα άτομα=Χημεία, πας με μαθηματικά να αναλύσεις την οικονομική θεωρία=Οικονομία

Συνεπώς τα μαθηματικά είναι η βάση δηλαδή η θεωρία και η εφαρμογή γίνεται από τις άλλες επιστήμες.

Και μη μου πουν μερικοί μα και στα μαθηματικά γίνεται εφαρμογή....π.χ. αποδείξεις θεωρημάτων ή άλλες θεωρίες. Δε γίνεται. Γιατί πολύ απλά υπάρχουν θεωρίες, ή λύνεις προβλήματα, αλλά μέχρι εκεί. Δεν επεκτείνεσαι. Αναλύεις μαι συνάρτηση, αλλά εφαρμόσιμα δε γίνεται κάτι.
Ενώ αν τα εφαρμόσεις ξέρω γω σε μαι θεωράι της Φυσικής, η εφαρμογή της είναι ξέρω εγώ το αποτέλεσμα της ταχύτητας ενός αυτοκινήτου.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[epote]

Και μη μου πουν μερικοί μα και στα μαθηματικά γίνεται εφαρμογή....π.χ. αποδείξεις θεωρημάτων ή άλλες θεωρίες. Δε γίνεται. Γιατί πολύ απλά υπάρχουν θεωρίες, ή λύνεις προβλήματα, αλλά μέχρι εκεί. Δεν επεκτείνεσαι. Αναλύεις μαι συνάρτηση, αλλά εφαρμόσιμα δε γίνεται κάτι.
Ενώ αν τα εφαρμόσεις ξέρω γω σε μαι θεωράι της Φυσικής, η εφαρμογή της είναι ξέρω εγώ το αποτέλεσμα της ταχύτητας ενός αυτοκινήτου.

τσου...

Να σου δωσω ενα παραδειγμα να καταλαβεις.

Το νομο της βαρυτητας τον ξερεις φανταζομαι F = GmM/R^2

Ο Newton κατεληξε στον νομο αυτο εμπειρικα, ητοι παρατηροντας την κινηση των πλανητων χρησημοποιησε τους νομους του kepler περι γωνιακης συχνοτητας και εκανε μια (πολυ καλη) μαντεψια για το ποια ειναι η ενταση της βαρυτητας.

Θα μπορουσε να ειχε καταληξει σε R^3 η R σκετο αλλα ηταν εξυπνος και τυχερος και κατεληξε στο σωστο R^2.

Tωρα εχε υποψη σου οτι αυτο που εκανε ο νιουτον ηταν ψιλο μαγεια, δεν ειχε ιδιαιτερο φορμαλισμο, ηταν αυτο ακριβως μια τυχερη και εξυπνη μαντεψια (an educated guess).

Καποια χρονια αργοτερα ενας κλαδος των μαθηματικων που ηταν προφανως αγνωστος στον νιουτον αναπτυχθηκε, η διανυσματικη αλγεβρα.

Στην διανυσματικη αλγεβρα λοιπων υπαρχει ενα θεωρημα που λεγεται "θεωρημα του γκαους".

Το θεωρημα αυτο αφορα την διασπορα ενος διανυσματικου πεδιου οταν αυτο βρισκεται μεσα σε μια τοπολογια σφαιρικα αναλοιοτη.

Λεει βασικα το εξις, η διασπορα του πεδιου μεσα στην επιφανια ισουτε με την ροη του πεδιου στην επιφανια.

Ειναι προφανες αυτο φυσικα, για να φανταστεις ενα μηχανικο αναλογο:

φαντασου οτι μεσα σε ενα μπαλονι βαζεις μια αντλια αερα και το φουσκωνεις, το φουσκομα ειναι η διασπορα. Το θεωρημα λεει το εξις προφανες:

Αν η επιφανια του μπαλονιου ηταν τρυπια πχ, ο αερας που θα εβγαινε ΕΞΩ απο την επιφανια του μπαλονιου (ροη) θα ηταν ισος με τον αερα που τρομπαρεις μεσα στο μπαλονι.

Duh τιποτα περιεργο.

Τεσπα αυτο ειναι ενα καθαρα μαθηματικο θεωρημα, δεν εχει καμια φυσικη εφαρμογη μεχρι εδω απλα μας λεει οτι το διπλο ολοκληρομα του καθετου διανυσματος στην επιφανια ισουτε με το τριπλο ολοκληρομα της διασπορας του διανυσματικου πεδιου μεσα στην επιφανια:

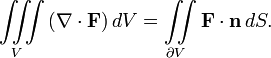
σε γλυτωνω ορισμενα μαθηματικα και σου λεω το εξις:

Το βαρυτικο πεδιο ειναι διανυσματικο προφανως γιατι αν βαλεις ενα σωμα μεσα σε ενα βαρυτικο πεδιο αυτο θα δεχθει μια δυναμη επανω του και δυναμη εχει μετρο κατευθυνση και φορα αρα ειανι διανυσμα.

Συνεπως ενα σωμα με σφαιρικα αναλοιοτη τοπολογια (η γη για παραδειγμα που ειναι σφαιρα) θα εχει στην επιφανια της (και εξω απο αυτη) συμφωνα με το θεωρημα διανυσματικη ροη ιση με τον ΟΓΚΟ της. (Διπλο ολοκληρομα = επιφανια, τριπλο = ογκος)

Κανοντας τις σχετικες πραξεις (και λαμβανοντες ορισμενες παραδοχες που σχετιζονται με το εσφαλμενο του νομου του νευτωνα) μπορεις απο αυτο το θεωρημα να καταληξεις στον νομο της παγκοσμιας ελξης.

Τι παραδοχες πρεπει να κανεις? Τεχνικοτητες που αφορουν το γεγονος οτι η βαρυτητα δεν ειναι συντηριτικη δυναμη και αγνοοντας τη συστροφη κτλ του πεδιου.

Τωρα θα μου πεις γιατι τα αγνοεις αυτα? Ε τα αγνοεις για να καταληξεις στην εξισωση του νιουτον αν δεν τα αγνοησεις...πας στην γενικη σχετικοτητα

και σε ρωτω, τα σχετικα μαθηματικα που εκανε ο γκαους και ολοκληρη η διανυσματικη αλγεβρα ηταν τελειως χωρις νοημα? Δεν ειχαν καμια εφαρμογη?

Να το θεσω ως εξις:

το χρωμα τι σχεση εχει με τον πινακα? Θα μπορουσε να υπαρξει ο πινακας χωρις το χρωμα?

Η αναλογια που χρησημοποιω ειναι σαθρη γιατι οταν λεω πινακας εννοω την ΥΠΑΡΞΗ και ΟΧΙ την θεωρια της φυσικης

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.